Magnetic field of a permanently magnetized cylinder

[LCSphysicist]

Homework Statement

.

Relevant Equations

/

I need to find the magnetic field of a permanently magnetized cylidner:

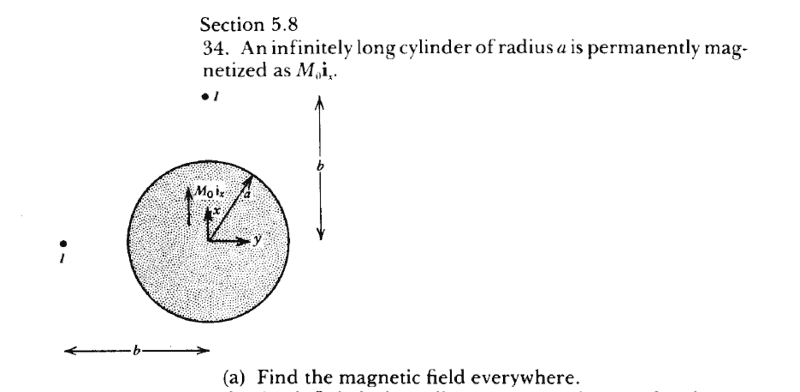
In calculating the magnetic field, i find that it should be $M_{0} \mu / 2$ and $H = M_{0} / 2$ inside. I just want to make sure that i understand the concepts in this type of problems.
Since $M = H \chi (1)$, does this mean that $\chi = 0.5$? Or (1) just apply to objects that have non permanently magnetization?

Also, i was not able to find the field outside the cyinder. Someone could help me?

 

[Charles Link]

The solution inside the cylinder is a well-known one: Using $B=\mu_o H +M$ rather than $B=\mu_o(H+M)$, the $H$ is uniform and is $H=-M_o/(2 \mu_o) \hat{i}$. The calculation of $B$ is then straightforward.

The field outside the cylinder is more complicated, and Legendre methods are usually used to determine the field, but I think Griffith's uses a simpler approach in one of his problems. See https://www.physicsforums.com/threa...ormly-polarized-cylinder.941830/#post-5956930

 

[alan123hk]

I agree that $~B=\mu_o H +M~$, and at the same time the magnetization current density must be defined as $J_m=\nabla \times M/\mu_o ~~$ instead of $~~J_m=\nabla \times M ~$, and the magnetic dipole moment of small amperian loop of current should be $~\mu_o SI ~$ instead of $~SI$.

I believe this will make Maxwell's equations with magnetic charges completely symmetric.

 

[Charles Link]

I think I have worked out the solution for the $H$ field outside of the cylinder, but the OP needs to show some effort of their own. One thing worth mentioning is that it involves working with a magnetic potential whose minus gradient is the $H$ field. The potential is continuous across the boundary, but separate solutions are necessary for $V_{inside}$ and $V_{outside}$.

Just an additional comment: I think it is also possible to work this problem using a potential for $B$, but in that case, rather than having the potential continuous across the boundary, it is necessary to have the $B$ field be continuous across the boundary.

 

[hutchphd]

This is an infinitely long cylinder with uniform magnetization.

 

[Charles Link]

This is an infinitely long cylinder with uniform magnetization.

The magnetization is perpendicular to the axis of the cylinder. It's a somewhat difficult problem.

 

[hutchphd]

Went right past me thanks!

 

[Charles Link]

I needed to do a google to see what the expansion looked like in cylindrical coordinates. It is not the Legendre Polynomials that appear in spherical coordinates, but there are similarities. See https://faculty.kfupm.edu.sa/phys/imnasser/Phys_571/Cylinder_coordinates_T131N.pdf

Getting the solution for the potential then involves making an Ansatz (German)=assumption for a trial solution, and if it can be shown to work, it then is the correct solution.

Here is where I ask the OP @Herculi to at least give it a try to see if they can come up with the right solution. I'd be glad to give a hint or two, if they get stuck. One hint is that $H_{inside}$ is basically known, (=use the well-known result that $H_{inside}=-\frac{M_o}{2 \mu_o} \hat{i}$), so that $V_{inside}$ should be fairly easy to figure out. Comparing it to the analogous electrostatic problem can also be very helpful. You also need the gradient in cylindrical coordinates, but you can google that.

 

[kuruman]

I have not solved this in detail (where the devil usually is) but the approach I would try first would be to use the magnetic scalar potential. The general, $z$-independent, solution to Laplace's equation has terms $1,~ \ln(r),~r^{n}\cos(n\theta),~ r^{n}\sin(n\theta),~r^{-n}\cos(n\theta),~ r^{-n}\sin(n\theta).$ I would toss out the unphysical terms and match boundary conditions.