- #1
ovoleg
- 94
- 0
Hello guys. I just had a question about the below problem. I am not sure if this is right but more likely it is wrong. I have been trying this problem for an extensive period of time now. If anyone could help out I would greatly appreciate it.
Following the dashed lines I showed the work that I did to solve this.
Question: Figure below is an end view of two long, parallel wires perpendicular to the xy-plane. Each carries a current I, but in opposite directions. (X means into the mage and the dot is out of the page).
Derive the expression for the magnitude of B at any point on the x-axis in terms of the x-coordinate of the point. What is the direction of B?
Click on this link to view the picture I copied.
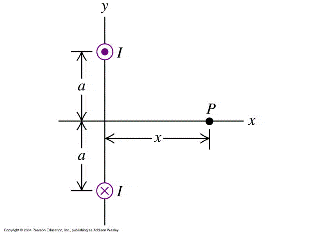 --------
--------
This is what I tried~~~
By right hand rule the vector would be upward and both of the magnetic fields from the two wires will add.
The field due to a long, straight, current-carrying conductor is B=mu_0I/2(pi)r where r is the distance from the wire to the point P.
The distance there is r=sqrt(a^2+x^2) from both conductors. By using superposition and adding vectors we can find the field B.
Thus Btotal=B1+B2
B1=Mu_0*I/(2*pi*sqrt(a^2+x^2))
B2=Mu_0*I/(2*pi*sqrt(a^2+x^2))
B1+B2= 2*Mu_0*I/(2*pi*sqrt(a^2+x^2))
B1+B2= Mu_0*I/(pi*sqrt(a^2+x^2))
Is this not correct?
Following the dashed lines I showed the work that I did to solve this.
Question: Figure below is an end view of two long, parallel wires perpendicular to the xy-plane. Each carries a current I, but in opposite directions. (X means into the mage and the dot is out of the page).
Derive the expression for the magnitude of B at any point on the x-axis in terms of the x-coordinate of the point. What is the direction of B?
Click on this link to view the picture I copied.
This is what I tried~~~
By right hand rule the vector would be upward and both of the magnetic fields from the two wires will add.
The field due to a long, straight, current-carrying conductor is B=mu_0I/2(pi)r where r is the distance from the wire to the point P.
The distance there is r=sqrt(a^2+x^2) from both conductors. By using superposition and adding vectors we can find the field B.
Thus Btotal=B1+B2
B1=Mu_0*I/(2*pi*sqrt(a^2+x^2))
B2=Mu_0*I/(2*pi*sqrt(a^2+x^2))
B1+B2= 2*Mu_0*I/(2*pi*sqrt(a^2+x^2))
B1+B2= Mu_0*I/(pi*sqrt(a^2+x^2))
Is this not correct?
Last edited: