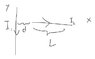
- #1
Antonius
- 49
- 0
Homework Statement
Homework Equations
Biot-Savart Law: ## dB = μIdl/4πr^2
F = ILxB
The Attempt at a Solution
I have not tried to solve it. BUT, please check my approach. I want to make sure my method is correct and whether there is a flaw or no.
I am trying to set up an integral here. I am to integrate it from from ## d+L ## to ## d ##. To do so, I will ignore the current in ## I_2 ## while integrating. Then, once I found ## B ## created by ## I_1 ## (which is "into the plane." [Meaning force acting on ## I_2 ## is in the same direction as ## I_2 ##
What is wrong up until now?
Well, here I am not sure how to find F acting on ## I_2 ##... Does ## F = IL(dot)B ## work?
Thank you.