- #1
kmarinas86
- 979
- 1
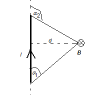
In consideration of a lone wire element of differential length dL carrying a current I:
Two things concern me here:
1) Is a magnetic field generated by current I really limited to only spaces that exist orthogonally to the line between the two ends of the wire element? If not, what does the magnetic field generated to the sides of these ends (and outward) look like?
2) How does one draw the equipotential surface of the magnetic field around such a lone wire element? What shape is it? Is it normally accepted that lines of magnetic force can be parallel to the magnetic equipotential surface, or does the conventional wisdom say that this does not happen? Normally, I thought that the lines of force must be perpendicular to the equipotential surface, but perhaps that is not really true since the circular magnetic field lines around a wire do not appear to cut equipotential surfaces of the magnetic field as far I am aware of. If equipotential surfaces correspond only to a scalar potential, then it relates only to line density of the magnetic field, which I know decreases with distance from the wire. I cannot see how conventional wisdom can take that as given and yet say that the lines of force are perpendicular to the equipotential of the magnetic field. So what do they really say?
Two things concern me here:
1) Is a magnetic field generated by current I really limited to only spaces that exist orthogonally to the line between the two ends of the wire element? If not, what does the magnetic field generated to the sides of these ends (and outward) look like?
2) How does one draw the equipotential surface of the magnetic field around such a lone wire element? What shape is it? Is it normally accepted that lines of magnetic force can be parallel to the magnetic equipotential surface, or does the conventional wisdom say that this does not happen? Normally, I thought that the lines of force must be perpendicular to the equipotential surface, but perhaps that is not really true since the circular magnetic field lines around a wire do not appear to cut equipotential surfaces of the magnetic field as far I am aware of. If equipotential surfaces correspond only to a scalar potential, then it relates only to line density of the magnetic field, which I know decreases with distance from the wire. I cannot see how conventional wisdom can take that as given and yet say that the lines of force are perpendicular to the equipotential of the magnetic field. So what do they really say?