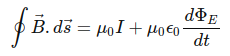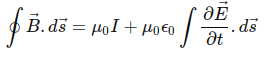Magnetic field when the area of the plates of a capacitor increases

[gabriel109]

When a current flows into or out of the capacitor plates, a magnetic field is created between them. Even though there are no charges flowing in the space between the plates, there is still a magnetic field and the source of that field is an uncharged current called a “displacement current”.
Suppose that the parallel plate capacitor with area A is fully charged with a charge Q and disconnected from the source. Then the area of the plates is doubled, then the charge Q will be distributed over twice the initial surface which gives us a smaller electric field E/2. Does this variation in the electric field produce a magnetic field?

It depends on which formula I analyze it with and I see a different result.
Using the Ampere-Maxwell equation with the derivative of the electric flux:

there is no variation in the electric flux since the area doubles but the electric field decreases by half (that is, I have the same initial flux EA) so the right side of the equation is equal to zero.
On the other hand, if I take into account the partial derivative of the electric field:

there is a change since the electric field decreases by half so the right hand side of the equation is not equal to zero.
I am getting different results. Where am I going wrong?

 

[kuruman]

It seems that you are using $d\vec s$ in the second equation for two different entities. On the right hand side it should be a directed area element on the surface through which there is electric flux. On the left hand side it should be a directed line element on the closed loop boundary of said surface (see picture below.) To see that consider how one gets from $\dfrac{d\Phi_E}{dt}$ in the first equation to the integral in the second.
Look at the picture below. The correct form of the equation in terms of that picture should be $$\oint\vec B \cdot d\vec l=\mu_0I+\mu_0\epsilon_0\int_{S_2}\frac{\partial \vec E}{\partial t}\cdot d\vec S_2$$ Here $d\vec l$ is the line element shown as a red arrow on the Amperian loop and $d\vec S_2$ is an area element (not shown) on the bulging surface $S_2$.

 

[Baluncore]

Suppose that the parallel plate capacitor with area A is fully charged with a charge Q and disconnected from the source. Then the area of the plates is doubled, then the charge Q will be distributed over twice the initial surface which gives us a smaller electric field E/2. Does this variation in the electric field produce a magnetic field?

When you change the area of the plates, the static charge on the plates will be redistributed to cover the greater area. That movement of charge is a current, so it will generate some magnetic field.

Perhaps you should consider changing the separation of the plates, then no charge will flow and there will be no magnetic field generated. The change in area will change the capacitance and so the static voltage.

 

[gabriel109]

It seems that you are using $d\vec s$ in the second equation for two different entities. On the right hand side it should be a directed area element on the surface through which there is electric flux. On the left hand side it should be a directed line element on the closed loop boundary of said surface (see picture below.) To see that consider how one gets from $\dfrac{d\Phi_E}{dt}$ in the first equation to the integral in the second.
Look at the picture below. The correct form of the equation in terms of that picture should be $$\oint\vec B \cdot d\vec l=\mu_0I+\mu_0\epsilon_0\int_{S_2}\frac{\partial \vec E}{\partial t}\cdot d\vec S_2$$ Here $d\vec l$ is the line element shown as a red arrow on the Amperian loop and $d\vec S_2$ is an area element (not shown) on the bulging surface $S_2$.
View attachment 353921

Thank you, I have already modified the nomenclature to avoid confusion with the differential elements.
The equality that confused me is the following:

I think I got it now, as the area of the plates increases both equations give zero.
The first equation gives zero because the electric flux does not vary in the time span that the area increases.
The second equation gives zero because in half of the "new area" the electric field decreases from E to E/2 but in the other half it increases from 0 to E/2. Adding the contributions we get zero.

 

[kuruman]

Thank you, I have already modified the nomenclature to avoid confusion with the differential elements.
The equality that confused me is the following:
View attachment 353926
I think I got it now, as the area of the plates increases both equations give zero.
The first equation gives zero because the electric flux does not vary in the time span that the area increases.
The second equation gives zero because in half of the "new area" the electric field decreases from E to E/2 but in the other half it increases from 0 to E/2. Adding the contributions we get zero.

Note that this thought experiment assumes that the capacitor is NOT connected to a battery as the area of the plates is doubled. Doubling the area doubles the capacitance. If this doubling happens with the plates connected to a battery, additional charge will flow from the battery into the capacitor because $Q=CV$ and $V$ is constant while $C$ doubles. Flowing charge means current $I$ will flowing in the wires connecting the plates to the battery which means displacement current $I_d$ in the gap between the plates.

 

[gabriel109]

Note that this thought experiment assumes that the capacitor is NOT connected to a battery as the area of the plates is doubled. Doubling the area doubles the capacitance. If this doubling happens with the plates connected to a battery, additional charge will flow from the battery into the capacitor because $Q=CV$ and $V$ is constant while $C$ doubles. Flowing charge means current $I$ will flowing in the wires connecting the plates to the battery which means displacement current $I_d$ in the gap between the plates.

Yes, one of the assumptions of my experiment is that it is not connected to a battery. In that case, does my conclusion that there is no variation in electric flux make sense? It starts with a flux $EA$ and ends with $EA$.

In the case you mention that it is connected to a battery, I understand the same thing you say. By doubling the area, the capacitance is doubled. That is, the magnitude of the electric field will continue to be $E$ but in twice the area than before. Therefore there would be a variation in electric flux that accounts for the displacement current between the plates. It starts with an electric flux $EA$ and ends with $2EA$.

 

[gabriel109]

Up . I just want a confirmation of my last reply.

 

[kuruman]

I think it is safer to think in terms of whether additional charge does or does not accumulate on the plates over a time interval. Charge accumulation means the existence of a "real" current which can be recorded with an ammeter. This leads one to deduce that there must be a "displacement" current across the capacitor plates to complete the circuit. This was Maxwell's reasoning and is more general than considering doubling the plate area.