Magnetic force on a curved conductor

[carnot cycle]

Homework Statement

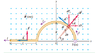
Find the total magnetic force on the semi-circular part of the conductor. There is a current I running counterclockwise through the semi-circle. The magnetic field B is out of the page.

Homework Equations

F = Il x B
l = Rθ
dl = Rdθ

The Attempt at a Solution

I assumed that the force is anywhere perpendicular to the conductor, so I disregarded the cross product and used F = IlB, where l is the length of the conductor. So,

dF = IBdl = IBRdθ

I then went ahead and integrated the dθ (upper limit: pi, lower limit: zero) and retrieved an answer of pi*IBR for the total force.

The book states that the answer is 2*IBR, and they get this answer by breaking up the dF force into an x-component IBRcosθdθ and a y-component IBRsinθdθ and then integrating these two components from lower limit of zero to upper limit of pi. Why is it necessary to break the dF into x and y components and integrating these components, rather than just integrating the total force dF? I've thought about it for a while but can't figure out why my method was incorrect. Thanks.

 

[TSny]

The force on each element is a vector. The total force is the sum of vectors for all elements.

When adding vectors, the magnitude of the result is not generally equal to the sum of the magnitudes of each vector. But the x-component of the result is equal to the sum of the x-components of the vectors, etc.