Magnetic Force on Moving Parallel Plate Capacitor

[jason.maran]

Homework Statement

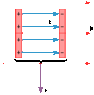
The drawing shows a parallel plate capacitor that is moving with a speed of 31 m/s through a 4.0 T magnetic field. The velocity v is perpendicular to the magnetic field. The electric field within the capacitor has a value of 170 N/C and each plate has an area of 7.5 multiplied by 10 x 10^-4 m^2. What is the magnetic force (magnitude and direction) exerted on the positive plate of the capacitor?

Homework Equations

F = Bqvsin(theta) --- sin() isn't important in this case because it's perpendicular

Then there's also E = F/q and C = KE_oA/d, but I can't for the life of me figure out how to use it in this case.

The Attempt at a Solution

Well, I've established that I'm going to need to find the charge somehow from the electric field and the area of the plates, since all the other info for F = Bvq is given. I'm at a loss to figure out how to get the charge though... thanks in advance for any help/advice.

 

[swuster]

You're completely correct. As it turns out, if you draw a Guassian cylinder or cube that extends halfway into one of the (conducting) capacitor plates and apply Gauss's Law, you'll find that the electric field from one plate is always \sigma/2\epsilon_0, where \sigma is the charge density of the plate (charge over area). If you add to this value the field from the other plate, you'll find that inside a parallel plate capacitor, the electric field always has a value of \sigma/\epsilon_0. So given your value for the electric field and the areas of the plates, you can now calculate the charge on the positive plate.

 

[jason.maran]

Thanks for your help, swuster. I'm still having a bit of trouble though.

I've done the following now:

E = (q/A)/2Eo
170 = (q/7.5e-4)/(2 * 8.85e-12)
q = 2.25e-12 C

Then I substitute in and solve for F:
F = qvB = (2.25e-12)(31)(4) = 2.79e-10 N, which is wrong, unfortunately.

I feel like I missed a step when following your instructions, and I didn't quite follow this bit:

If you add to this value the field from the other plate, you'll find that inside a parallel plate capacitor, the electric field always has a value of LaTeX Code: \\sigma/\\epsilon_0 .

Thanks again for the help, I appreciate it greatly! :)

 

[Sonolum]

E = (q/A)/2Eo

Should be:

E = (q/A)/Eo

^_^

 

[jason.maran]

Ah, OK, thanks a bunch! Worked like a charm after that!

 

[Sonolum]

Yep - between the capacitor plates, the electric field adds!