Magnetic Induction Through a Moving Wire

[Broem]

Homework Statement

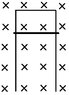
A very long u-shape conducting wire is placed vertically in a constant magnetic field. The magnetic field is perpendicular to the plane of the wire. The strength of the magnetic field is B = 0.9 tesla. A conducting rod is placed on the wire, as shown in the picture. The length of the rod is 7 m. The rod has a mass of 5 kg and a resistance of 8 Ohm. When the rod is released from rest, it start to slide down but maintain good contact with the u-shape wire. After some time, the rod reaches a maximum velocity and moves constantly thereafter. You can ignore the resistance of the u-shape wire and the friction between the rod and the wire.
B = 0.9T ; L = 7m ; R = 8Ω ; g= 9.8m/s
What is the maximum velocity of the moving rod?
What is the current in the loop when the moving rod reaches maximum velocity?

Homework Equations

ε= v*L*B
I=(v*L*B)/R
F = I*L*B

or
F = (v(L*B)^2)/R

The Attempt at a Solution

Ok I know that once this wire begins to move it creates an emf and a current. The magnetic force generated is going to counteract my force of gravity. My assumption is that when it reaches its maximum velocity the F will be 9.8 as well since it can no longer change.
So:
F = 9.8N?
I've tried plugging in from here and have not been able to get a correct answer, where am I going wrong?
9.8 = I(7)(0.9) thus I = 1.56A

1.56 = (v(7)(0.9))/8 thus v = 1.97m/s

 

[Broem]

As soon as I posted this I remembered that the F is ACTING on MASS. This makes my F = 49N
D'oh!
I'll leave this here I guess.
Plugging in it all worked out smoothly :)