amoghthebad
- 3
- 0
- Homework Statement
- Relationship between final velocity of a steel ball and magnetic field strength in a gauss cannon.
- Relevant Equations
- F = (μ * B^2 * V^2) / (2 * μ0 * d^2)
F = ma
v^2=u^2+2as
I have to write a physics research project, and the topic I chose is magnetism. More specifically, the relationship between the final velocity of a steel ball, and the magnetic field strength in a gauss cannon. However, for the part where I use mathematical formulas to predict the results, things have gone extremely downhill. The problem is that I have already conducted the experiment, and the values that I am getting mathematically are definetly not lining up with the actual experimental values.
The plan was to calculate the magnetic pull force using the first formula: F = (μ * B^2 * V^2) / (2 * μ0 * d^2)
This formula was taken directly from this site, as it seemed to be exactly what I needed: https://www.physicsforums.com/threads/calculate-magnetic-pull-force-for-steel-ball.743775/
μ, magnetic permeability of ferratic steel (the material of the ball) = 1.76*10^-3
V= Volume of the ball(cubic metre, m^3) = 4*10^-6
μ0= Magnetic Permeability of free space (Henries per Metre, H/m) =1.2566*10^-6
d= Distance between the ball and the magnet (metre, m) = 0.075
The values for B (magnetic field strength) were calculated using this calculator: https://www.kjmagnetics.com/fieldcalculator.asp
Orignally, the distance from the magnet was set to 75mm (75 using metric units on the y value in the calculator), however when that didnt work, I set it to the lowest distance I could for each thickness of the magnet, but that also didnt work.
Here is the table of thickness of the magnets with the field strength 75mm away from them

Then, the next step was to substitute the pull force value into the formula F=ma, to calculate the acceleration.
m=mass of the ball (Kilograms, kg) = 0.031

The image above is a picture of the final formula, and how I got it. At this point, I knew something was very wrong, as I realized the value of acceleration would be too small to make sense, and that the first formula (F = (μ * B^2 * V^2) / (2 * μ0 * d^2)) was no good.
The final step was to substitute the acceleration value into the formula v^2=u^2+2as to calculate v, and input v into the equation again in place of u for the second stage of the cannon, and input the result into the formula one last time for the three stages of the gaussian cannon.
However, the values that I am getting are very wrong.
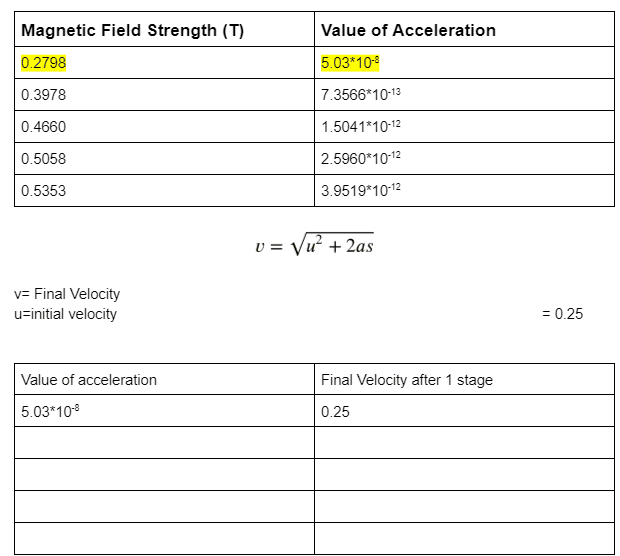
As obvious, the values of acceleration are way too small. As a result, the final velocity obtained is literally no different from the inital velocity.
I am pretty sure that the first formula is wrong, as the values for pull force that i am getting from it are way too small. For example, using the formula, the magnetic pull force value that I get for a magnet 5.001mm thick and 19mm wide (grade N35) is 5.01*10^-4. However using the magnetic pull force calculator from the same website, the pull force value that I get is 59.11 newtons.
So my request is: Can anyone explain to me why the formula isnt working, and what change I could make to the formula to make it work? Or is there another formula that I could use? I could simply just use the calculator from the site instead of a formula to get the pull force values, but I am afraid that the marker will think that it's too simple, and give me a low marking.
The plan was to calculate the magnetic pull force using the first formula: F = (μ * B^2 * V^2) / (2 * μ0 * d^2)
This formula was taken directly from this site, as it seemed to be exactly what I needed: https://www.physicsforums.com/threads/calculate-magnetic-pull-force-for-steel-ball.743775/
μ, magnetic permeability of ferratic steel (the material of the ball) = 1.76*10^-3
V= Volume of the ball(cubic metre, m^3) = 4*10^-6
μ0= Magnetic Permeability of free space (Henries per Metre, H/m) =1.2566*10^-6
d= Distance between the ball and the magnet (metre, m) = 0.075
The values for B (magnetic field strength) were calculated using this calculator: https://www.kjmagnetics.com/fieldcalculator.asp
Orignally, the distance from the magnet was set to 75mm (75 using metric units on the y value in the calculator), however when that didnt work, I set it to the lowest distance I could for each thickness of the magnet, but that also didnt work.
Here is the table of thickness of the magnets with the field strength 75mm away from them
Then, the next step was to substitute the pull force value into the formula F=ma, to calculate the acceleration.
m=mass of the ball (Kilograms, kg) = 0.031
The image above is a picture of the final formula, and how I got it. At this point, I knew something was very wrong, as I realized the value of acceleration would be too small to make sense, and that the first formula (F = (μ * B^2 * V^2) / (2 * μ0 * d^2)) was no good.
The final step was to substitute the acceleration value into the formula v^2=u^2+2as to calculate v, and input v into the equation again in place of u for the second stage of the cannon, and input the result into the formula one last time for the three stages of the gaussian cannon.
However, the values that I am getting are very wrong.
As obvious, the values of acceleration are way too small. As a result, the final velocity obtained is literally no different from the inital velocity.
I am pretty sure that the first formula is wrong, as the values for pull force that i am getting from it are way too small. For example, using the formula, the magnetic pull force value that I get for a magnet 5.001mm thick and 19mm wide (grade N35) is 5.01*10^-4. However using the magnetic pull force calculator from the same website, the pull force value that I get is 59.11 newtons.
So my request is: Can anyone explain to me why the formula isnt working, and what change I could make to the formula to make it work? Or is there another formula that I could use? I could simply just use the calculator from the site instead of a formula to get the pull force values, but I am afraid that the marker will think that it's too simple, and give me a low marking.