Magnitude of magnetic field at different points near a capacitor.

[zenterix]

Homework Statement

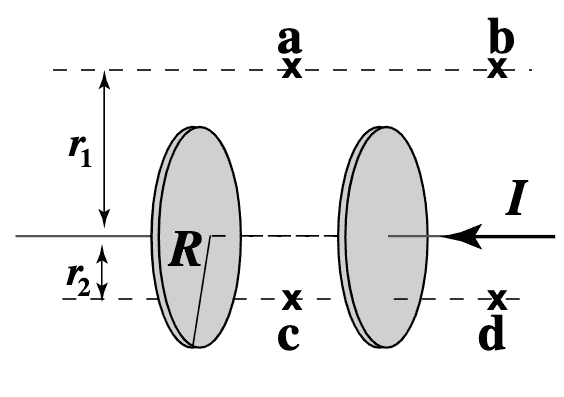
Consider a capacitor that is charging, as in the picture below. The capacitor is ideal (no edge effects).

Points $a$ and $b$ areat a distance $r_1>R$ with respect to the center line, and $c$ and $d$ are at a distance $r_2<R$.

Relevant Equations

Which of the following statements about $B$, the magnitude of the magnetic field, at points $a,b,c,$ and $d$ are true?

$B(a)>B(b)$
$B(a)<B(b)$
$B(a)=B(b)$

$B(c)>B(d)$
$B(c)<B(d)$
$B(c)=B(d)$

Here is a picture depicting the capacitor and the points of interest.

I approached this problem by applying the Ampere-Maxwell law.

For each point I used an circular Amperian loop that I denote by $P$, enclosing a circular surface $S$.

Thus, for point $b$ we have

$$\oint_{P_b}\vec{B}\cdot d\vec{s}=B_b2\pi r_1=\mu_0 I\implies B_b=\frac{\mu_0 I}{2\pi r_1}$$

Similarly, for point $d$

$$B_d=\frac{\mu_0 I}{2\pi r_2}$$

Next, I considered points $a$ and $c$.

The magnitude of the electric field between the plates is $\frac{q}{\epsilon_0 A}$ where $A$ is the area of a capacitor plate.

$$\oint_{P_a}\vec{B}\cdot d\vec{s}=B_a2\pi r_1=\mu_0\frac{d}{dt}\left (\frac{q}{\epsilon_0 A}\right )\pi R^2$$

$$=\frac{\mu_0 I\pi R^2}{\epsilon_0\pi R^2}$$

$$\implies B_a=\frac{\mu_0I}{\epsilon_0 2\pi r_1}$$

Similarly

$$B_c2\pi r_2=\mu_0\frac{d}{dt}\left (\frac{q}{\epsilon_0 A}\right )\pi r_2^2=\frac{\mu_0 I\pi r_2^2}{\epsilon_0\pi R^2}$$

$$=\frac{\mu_0 Ir_2^2}{\epsilon_0 R^2}$$

$$B_c=\frac{\mu_0 I r_2}{\epsilon_0 2\pi R^2}$$

These are my calculations currently. They seem incorrect. Having a $\epsilon_0$ factor in the denominator of these expressions seems incorrect at first glance given that the order of magnitude of this constant is $10^{-12}$.

 

[TSny]

The magnitude of the electric field between the plates is $\frac{q}{\epsilon_0 A}$ where $A$ is the area of a capacitor plate.

$$\oint_{P_a}\vec{B}\cdot d\vec{s}=B_a2\pi r_1=\mu_0\frac{d}{dt}\left (\frac{q}{\epsilon_0 A}\right )\pi R^2$$

What is the fundamental law that you are using to set up this equation? You might be missing a factor of $\epsilon_0$.

 

[kuruman]

If you are going to quote the Ampere-Maxwell law, quote it correctly. The displacement current term (Maxwell's correction) is $\mathbf J_d=\dfrac{\partial \mathbf D}{\partial t}=\dfrac{\partial (\epsilon_0 \mathbf E)}{\partial t}$. The $\epsilon_0$ in the numerator cancels the one in the denominator.

 

[zenterix]

You might be missing a factor of ϵ0.

Indeed you are correct. I forgot a factor of $\epsilon_0$.

$$\oint \vec{B}\cdot d\vec{s}=\mu_0\left (\iint_S \vec{J}\cdot\hat{n}dA+\epsilon_0\iint_S \vec{E}\hat{n}dA\right )$$

 

[TSny]

Indeed you are correct. I forgot a factor of $\epsilon_0$.

$$\oint \vec{B}\cdot d\vec{s}=\mu_0\left (\iint_S \vec{J}\cdot\hat{n}dA+\epsilon_0\iint_S \vec{E}\hat{n}dA\right )$$

OK, but here you forgot a time derivative.

 

[zenterix]

Indeed

$$\oint \vec{B}\cdot d\vec{s}=\mu_0\left (\iint_S \vec{J}\cdot\hat{n}dA+\epsilon_0\frac{d}{dt}\iint_S \vec{E}\hat{n}dA\right )$$

Fixing the original equations we have

$$B_a=B_b=\frac{\mu_0I}{2\pi r_1}$$

$$B_c=\frac{\mu_0I}{2\pi r_2}\frac{r_2^2}{R^2}$$

$$B_d=\frac{\mu_0I}{2\pi r_2}$$

Thus, $B_a=B_b$ and $B_c<B_d$.

 

[TSny]

Indeed
$$\oint \vec{B}\cdot d\vec{s}=\mu_0\left (\iint_S \vec{J}\cdot\hat{n}dA+\epsilon_0\frac{d}{dt}\iint_S \vec{E}\hat{n}dA\right )$$
Fixing the original equations we have

$$B_a=B_b=\frac{\mu_0I}{2\pi r_1}$$
$$B_c=\frac{\mu_0I}{2\pi r_2}\frac{r_2^2}{R^2}$$
$$B_d=\frac{\mu_0I}{2\pi r_2}$$
Thus, $B_a=B_b$ and $B_c<B_d$.

Looks good to me.