Magnitude of the Projection of force "F" on the u-axis

[mhrob24]

Homework Statement

Find the magnitude of the force PROJECTED on the U and V axes

Relevant Equations

Fx = F * cos(theta) OR dot product of F and Ufu (unit vector along u-axis)

So I was watching a YouTube video preparing for a quiz on Wednesday, and I saw something that I would like clarification on. I'm pretty sure I understand what is being explained, but I just want to confirm.

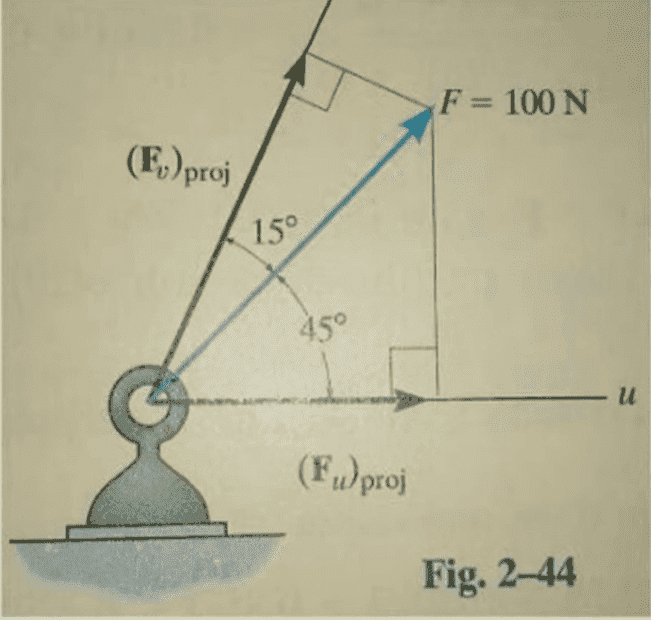The figure above is associated with the problem at hand. So I understand that to get the magnitude of the projection of a force vector that is parallel to some line, you can either use:

1. F_u = F * cos(theta)

OR

2. dot product of F and the unit vector along the parallel line (in this case, U_u)

So for this problem, using the first method, the two equations would be:

F_u = F * cos(45) AND F_v = F * cos(15)

I totally get that...what I am slightly confused about is what the professor says later in the video. He says:

"Note that the magnitude of the PROJECTION is NOT equal to the magnitudes of the COMPONENTS of this force. For that, you would need to use the parallelogram law and the law of sines".

Now, he's saying this because the axes here do not form a 90 deg angle? because for example, if the figure was like this:

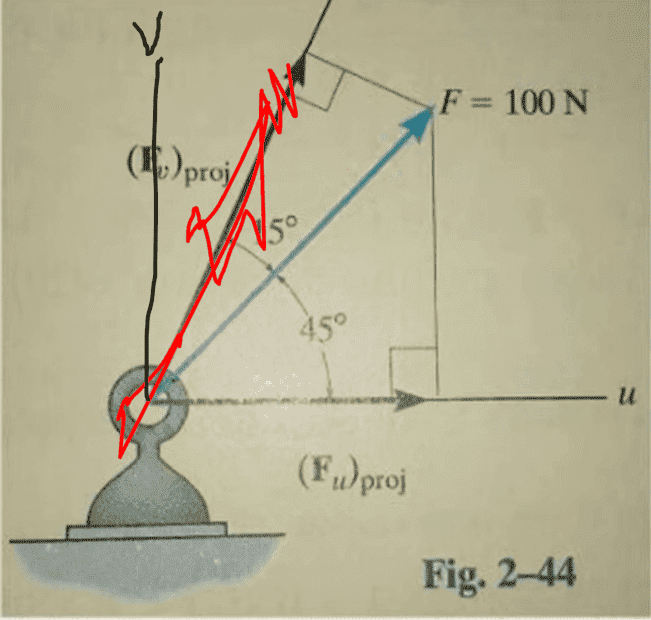
and the question asked us to find the magnitude of the COMPONENTS of the force F along the u and v axes, then the equation to find F_u would still be the same : F * cos(45)...BUT, the equation to find F_v would NOT be the same as before. It would now be: F * sin(45).So this is just a special case where it just so happens that the magnitude of the PROJECTION and the magnitude of the COMPONENT along the U-axis can be solved using the same equation : F * cos(45) ?FYI, here is the video:

 

[FactChecker]

Projection is a linear function. The projection of a vector onto another is equal to the sum of the projections of its components in any orthogonal axis system.