Magnitudes of the sum of two vectors

[keroberous]

This is a question that I saw in a textbook:

"If the magnitude of a+b equals the magnitude of a+c then this implies that the magnitudes of b and c are equal. Is this true or false?"

The textbook says that this statement is true, but I'm inclined to believe it is false. I made a quick sketch to show my thinking visually.

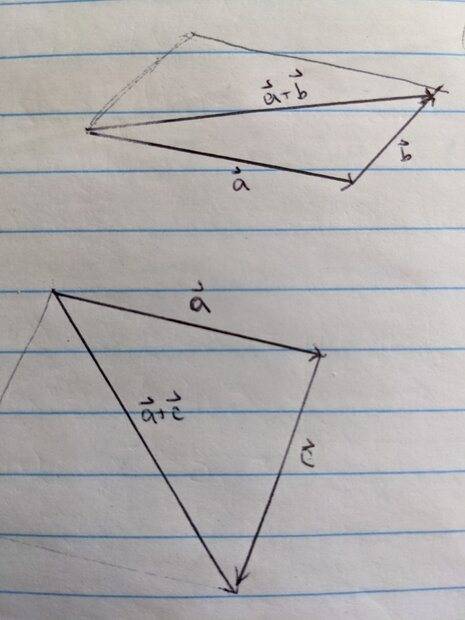
I drew these diagrams to scale, so vector a is the same in each case and the lengths of a+b and a+c are in fact equal (both 5 cm). It's clear to me that b and c are different lengths/magnitudes here. I'm not sure if the text made an error (not unheard of) or if I made an incorrect assumption somewhere. Thanks!

 

[DaveE]

 

[DaveE]

Suppose a=(2,0), b=(1,0), c=(-5,0) ...

 

[keroberous]

So your diagram isn't all that different than mine, so I take it then that the textbook is incorrect and the statement is false?

Here's the book's entire reasoning:

"true; |a+b| and |a+c| both represent the lengths of the diagonal of a parallelogram, the first with sides a and b and the second with sides a and c; since both parallelograms have a as a side and diagonals of equal length |b|=|c|"

 

[PeroK]

So your diagram isn't all that different than mine, so I take it then that the textbook is incorrect and the statement is false?

Here's the book's entire reasoning:

"true; |a+b| and |a+c| both represent the lengths of the diagonal of a parallelogram, the first with sides a and b and the second with sides a and c; since both parallelograms have a as a side and diagonals of equal length |b|=|c|"

It's hard to think of anything more wrong!

It's not even true in one dimension!

 

[DaveE]

Maybe you should get different textbook?

Edit: Oops. I just noticed this was a question in the book, not a statement. It's just a typo. So - never mind...

 

[keroberous]

It's hard to think of anything more wrong!

It's not even true in one dimension!

I'm glad I wasn't going crazy!

Maybe you should get different textbook?

If only that was an option. lol

Thanks!