Majorana representation of higher spin states

[fsh26]

TL;DR Summary

A discussion of the derivation of Majorana representation formulas for spins greater than 1/2 is proposed.

In the article by E. Majorana "Oriented atoms in a variable magnetic field", in particular, it's considered (and solved) the problem of describing a state with spin J using 2J points on the Bloch sphere.
That is, if

the general state of the spin system

, (1)
then, according to the article, those 2J points in on the Bloch sphere are described by the following complex numbers (

):

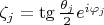. (2)

Here

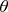- is the angle between the unit vector and the Z axis,

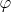- is the angle between the projection of the given vector (on the XY plane) with the X axis (Bloch spheres),

- are the roots of the polynomial

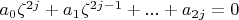, (3)

where

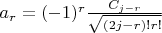. (4)

In the case of J=1/2, is very simple

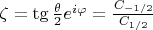(5)

Here

(

) can be considered as the probability of finding the end of the unit vector at the lower (upper) pole of the Bloch sphere, and

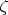- is a point of the complex plane that is drawn through the center given sphere (stereographic projection of the end of the unit vector from the south pole onto the given plane).

But, for the cases J>1/2, I encountered difficulties in following the idea of deriving (3) and (4). Of course, there are several papers where this representation of Majorana is used, but so far I have not found such a work where the derivation of formulas is discussed in detail. I will be grateful if you advise literature or sources that can help to clearly understand the derivation of formulas (3) and (4).

 

[vanhees71]

By googling I've found this paper. Maybe it's of help:

https://www.reed.edu/physics/facult...ssays/Angular Momentum, Spin/D2. Majorana.pdf

This presentation of the irreps of the SU(2) is pretty out of use, but it can be found in some math books, like

V. I. Smirnov, A course of higher mathematics, vol. III part 1, Pergamon press (1964)

Usually we derive the representation theory of the rotation group SO(3) and its covering group SU(2) using the commutation relations of the angular-momentum components by diagonalizing simultaneously $\hat{\vec{J}}^2$ and $\hat{J}_z$.