Man on a railroad car rounding a curve

[LCSphysicist]

Homework Statement

.

Relevant Equations

The friction equations

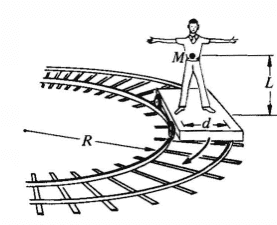
"A man of mass M stands on a railroad car which is rounding an
unbanked turn of radius R at speed v. His center of mass is height L
above the car, and his feet are distance d apart. The man is facing the
direction of motion. How much weight is on each of his feet?"

I came five equations, and five incognits:
Call the inside side with index i, outside with o

Ni + No = Mg
Ni*μ = mi*v²/R
No*μ = mo*v²/(R+d)
mi + mo = M
No*d/2 = No*μ*l + Ni*d/2 + Ni*μ*l

I will not develop, but you know that we can came to a answer to both N without μ.

The book came to this equations:

Ni + No = Mg
No*μ + Ni*μ = Mv²/R
No*d/2 = No*μ*l + Ni*d/2 + Ni*μ*l

The bold equations is where we desagree, if i could say, i'd say that book's solution is summarized, but justified if d is small in comparation, while my solution is more complete, but in some cases desnecessary. Example, F = Gmm/(r+d)² is the right, but F = m*g is a nice aproximation.

But, i don't know...

 

[wrobel]

Let $S$ be the center of mass and $\boldsymbol F_l, \boldsymbol F_r$ are the reactions from the trolley to the left and right leg respectively:
$$M\boldsymbol a_S=M\boldsymbol g+\boldsymbol F_l+\boldsymbol F_r.$$

The angle momentum equation
$$0=\boldsymbol r_l\times \boldsymbol F_l+\boldsymbol r_r\times \boldsymbol F_r,$$
here
$\boldsymbol r_r$ is a vector from the center of mass to the right sole,
$\boldsymbol r_l$ -- respectively

Introduce a coordinate frame moving with the trolley and expand the equations

 

[etotheipi]

Yes I agree with @wrobel, for an extended body the net radial force is proportional to the centre of mass radial acceleration, and the COM is performing circular motion at speed $v$ and radius $R + \frac{d}{2}$. For this NII equation, it doesn’t matter where the force is applied on the extended body.

I assume $d << R$ so we can essentially ignore the $\frac{d}{2}$.

If you hypothetically knew the net force on e.g. his foot, you could write down an equation for the circular motion of the centre of mass of his foot and this would evidently be at a different radius.

 

[wrobel]

Substitute $\boldsymbol F_l$ from the first equation to the second one:
$$\boldsymbol F_l=M\boldsymbol a_S-M\boldsymbol g-\boldsymbol F_r;$$
$$(\boldsymbol r_r-\boldsymbol r_l)\times \boldsymbol F_r=M\boldsymbol r_l\times(\boldsymbol g-\boldsymbol a_S)$$
From the last equation $\boldsymbol F_r$ is determined up to additional horizontal vector directed radially. The vertical component of $\boldsymbol F_r$ is determined correctly

 

[PeroK]

The book came to this equations:

Ni + No = Mg
No*μ + Ni*μ = Mv²/R
No*d/2 = No*μ*l + Ni*d/2 + Ni*μ*l

The bold equations is where we desagree, if i could say, i'd say that book's solution is summarized, but justified if d is small in comparation, while my solution is more complete, but in some cases desnecessary. Example, F = Gmm/(r+d)² is the right, but F = m*g is a nice aproximation.

But, i don't know...

I agree with the book's solution, except:

1) $R \rightarrow R + \frac d 2$, as pointed out above.

2) The specific friction force on each foot is indeterminate. $\mu N$ is the maximum possible force of static friction, but it's only the sum of the friction forces that matters.

 

[wrobel]

I believe this problem still needs some extra explanation.

Actually the angular momentum equation for a rigid body (for the man here) is written as follows
$$J_S\boldsymbol{\dot \omega}+\boldsymbol\omega\times J_S\boldsymbol\omega=\boldsymbol r_l\times\boldsymbol F_l+\boldsymbol r_r\times\boldsymbol F_r.\qquad (*)$$
Here $J_S$ is man's inertia operator about his center of mass. By the conditions of the problem the angular velocity is constant: $\boldsymbol{\dot \omega}=0$. This kills the first term in the left side of (*).

Further we implicitly assume that the man stands as a symmetric sculpture: the vertical axis passing through his center of mass is a principal axis for $J_S$ that is $J_S\boldsymbol\omega=\lambda\boldsymbol\omega.$ This assumption kills the second term in the left side of (*)

If the man takes down one hand or inclines aside or takes nonsymmetric pose somehow else then $\boldsymbol\omega\times J_S\boldsymbol\omega\ne 0$.