- #1
Soren4
- 128
- 2
I wonder if it is correct to read an open air manometer in the case of viscous fluid in the following (usual) way. Consider the situation showed in the picture where a viscous fluid is flowing, in fact ##z_C <z_A##.
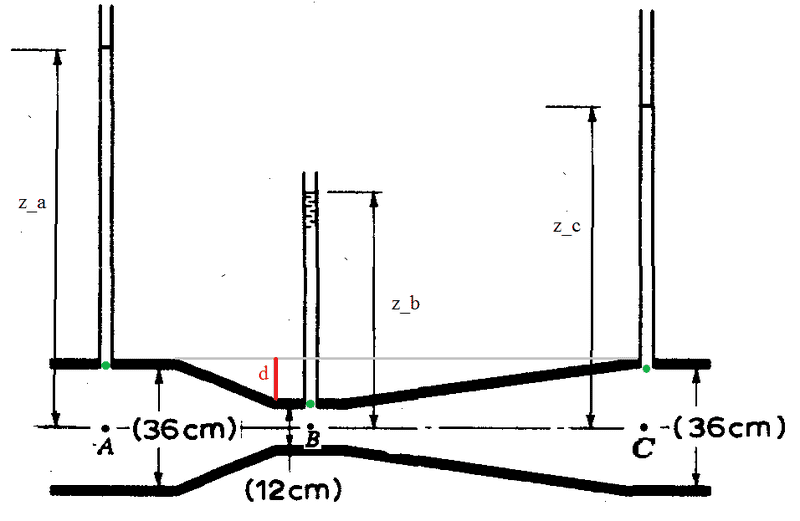
The reading of the manometer would be ##p_a=\rho g z_a##, ##p_b=\rho g z_b##, ##p_c=\rho g z_c##,
The main problem is that, while the black points ##A##, ##B## and ##C## are at the same heights, the fluid in ##B## is in the manometer for an height ##d## more than the fluid in ##A## and ##C## (or equivalently, the corresponding green points are not at the same height).
In the manometer the fluid is not moving, so I have no problem in writing that ##\Delta p=\rho g h##, but inside the tube the fluid is moving and therefore the variation of pressure with height would be different.
That would not be a problem if the green points were at the same height or in the case of validity of Bernoulli equation because ##\Delta p=\rho g h## would still be valid along vertical lines (even if the fluid is in motion).
But here Bernoulli equation cannot be used, since the fluid is viscous, so my question is: can I read the manometer referring heights to the horizontal line in the middle of the tube, or is there some other way to read it.
Furthermore I would like to know if there is a precise relation between the pressure in the green points and the pressure at black points. As said before, in the case of non viscous fluid, the pressures would be equal there, but what about this case?
The reading of the manometer would be ##p_a=\rho g z_a##, ##p_b=\rho g z_b##, ##p_c=\rho g z_c##,
The main problem is that, while the black points ##A##, ##B## and ##C## are at the same heights, the fluid in ##B## is in the manometer for an height ##d## more than the fluid in ##A## and ##C## (or equivalently, the corresponding green points are not at the same height).
In the manometer the fluid is not moving, so I have no problem in writing that ##\Delta p=\rho g h##, but inside the tube the fluid is moving and therefore the variation of pressure with height would be different.
That would not be a problem if the green points were at the same height or in the case of validity of Bernoulli equation because ##\Delta p=\rho g h## would still be valid along vertical lines (even if the fluid is in motion).
But here Bernoulli equation cannot be used, since the fluid is viscous, so my question is: can I read the manometer referring heights to the horizontal line in the middle of the tube, or is there some other way to read it.
Furthermore I would like to know if there is a precise relation between the pressure in the green points and the pressure at black points. As said before, in the case of non viscous fluid, the pressures would be equal there, but what about this case?