Manometer Reading using Fluid Dynamics

[RMalt]

Homework Statement

so I have been working on this problem :

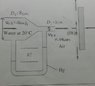
1. Diameter1 at wide end: 8cm || V1 = 1.56m/s
2. Diameter2 at narrow end: 3cm || V2 = 11.094m/s
3. Force exerted on plate = 87N

Find the manometer reading

Picture below:

Homework Equations

P1+(1/2 ρv1^2)=P2+(1/2 ρv2^2)

1 − 2 = (2 −1)ℎ

The Attempt at a Solution

I know that due to Bernoulli's Equation the pressure where velocity is at 11.094m/s is much lower than at the other end. This can also be seen from the Mercury(Hg) level.

I have take P2 as being 0 because it is open to the atmosphere -- I am unsure whether this should be taken as 0 or 1.

I have used the following equation to work out P1 :

P1+(1/2 ρv1^2)=P2+(1/2 ρv2^2) and I end up with P1 = 4.5581(atm??)

Can I use : 1 − 2 = (2 −1)ℎ in order to find the height ? Or is thus equation only valid for a differential manometer that has a constant cross sectional area ?

I am still unsure how to proceed in this case. Any help or tips would be appreciated.

 

[CivilSigma]

Yes, P2 should be taken as 0.
I agree with your velocity calculations.
When I solved the Bernoulli equation, I got P1 = 60.3 kPa. I suggest you work in metric units, so keep pressure in units of Pa.

To find the value of h , I made the following simplifying assumption, the pressure at the end of the manometer is as well 0 even though the system is not
exposed to the atmosphere.

Then, to solve for h, I set a new datum at the highest level of mercury in the tube and solved:

$$ P_1 + \rho_w \cdot h - \rho_{Hg}\cdot h = P_2$$
$$h = \frac{P_1}{\rho_{Hg} - \rho_{w}}$$
$$h= 4.8 m$$

The value of h looks too large... but I hope this was insightful.

Edit: Was v1 calculated or was it given?

 

[RMalt]

Hi, thanks for your time and insight on this matter. However, unfortunately this is not one of my strong subjects. I re-worked some calculations and got P1 = 60.3kPa as is yours.

Can I use the formula ρ*Hg*h = p1 ? I found this other formula not taking into consideration the density of water. You think this is incorrect ?

The answer comes to 4.437 m. Still pretty big. EDIT: NO I CAN'T

Edit: V1 was found, I cross-checked this with someone else and it appears to be correct. I used :

F = v^2 *ρ *A2 to find Velocity at thin end of pipe and then found V1 using A1V1 = A2V2

 

[RMalt]

Edit: Was v1 calculated or was it given?Calculated

 

[RMalt]

I think i found a mistake in your calculation: Shouldnt you also be dividing by gravity ?? 1 − 2 = (2 −1)ℎ

 

[CivilSigma]

I think i found a mistake in your calculation: Shouldnt you also be dividing by gravity ?? 1 − 2 = (2 −1)ℎ

Yes thank you for pointing that out!
Then the final answer would be 0.489 m which is more reasonable!

In regards to how I got the equation, it's not sufficient to only have ρ*Hg*h = p1 because there are two liquids that contribute to the change of pressure in the manometer. Taking the datum at the highest level of Hg, and knowing that pressure increases with depth, we have:

Original pressure in pipe , P_1, then it increases by $\rho \cdot g \cdot h$ which is due to the water. Then it increases by some value attributed to mercury, loops around and decreases by the same value attributed to mercury and finally keeps decreasing by a value of height 'h' attributed to mercury (because we are going up) to give us the final pressure P2.
.

 

[gneill]

Hi RMalt,

Edit: V1 was found, I cross-checked this with someone else and it appears to be correct. I used :

F = v^2 *ρ *A2 to find Velocity at thin end of pipe and then found V1 using A1V1 = A2V2

You should only list actual given values in the problem statement and show any derived values in the solution attempt. Otherwise helpers won't know what was is part of the original problem as it was given to you and what might need checking. You might also provide a bit more descriptive text for the setup so that the nature of the problem is clear. What density values did you use for water and mercury? Were they given values or were you expected to look them up?

Basically, assume that the person helping you has never seen the problem before and will want to work it out using exactly the information that you were given.

It's good to see that you arrived at what appears to be a reasonable answer.

@sakonpure6, please be careful about doing too much of the work for the OP. Helpers are not allowed to provide complete solutions or do the work for the person requesting help. Hints, references to related materials, pointing out calculation errors, and general guidance are fine. All this is explained in the forum rules.