- #1
Firepanda
- 430
- 0
I am doing question 2 here:

My solution so far is this:
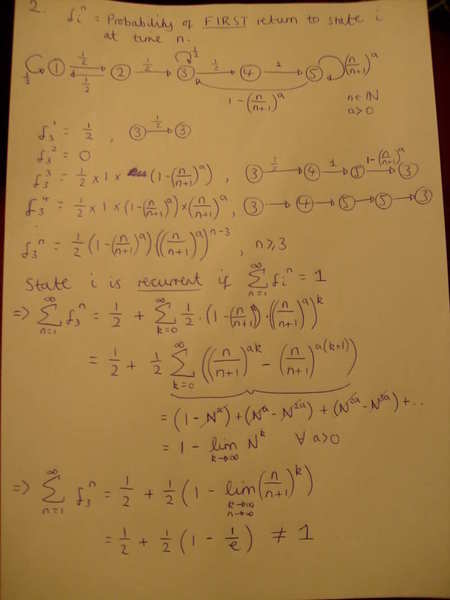
Where have I gone wrong? I'm assuming I'm taking the wrong limit but I'm really stumped here and no idea what else it should be..
I hope my writing is ok, I tried to be as neat as possible!
Thanks
My solution so far is this:
Where have I gone wrong? I'm assuming I'm taking the wrong limit but I'm really stumped here and no idea what else it should be..
I hope my writing is ok, I tried to be as neat as possible!
Thanks