Markov model to find the probability of a Pepsi drinker buying a Coke?

[shivajikobardan]

Homework Statement

Find the probability of using coke for a current pepsi user in 4th purchase?Markov Model problem.

Relevant Equations

Transition Probability Matrix

Design the markov model and transition matrix for the given data. Answer the following questions based on the mode.
a) If a person purchase coke now the probability of purchase of coke next time is 80%.
b) If a person purchases pepsi now the probability of purchasing pepsi next time is 70%.

Then,
Find the probability of using coke for a current pepsi user in 4th purchases-:

My solution-:

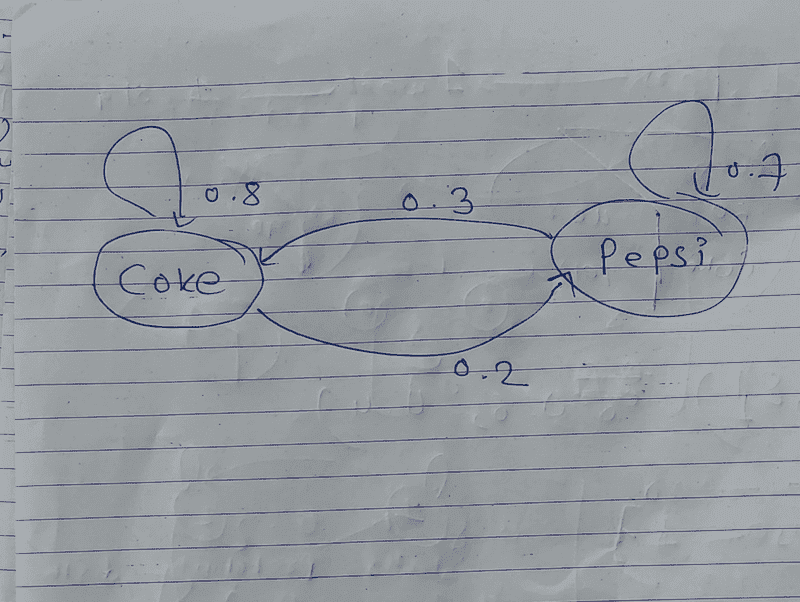
This is the transition diagram.

This is the transition probability matrix-:

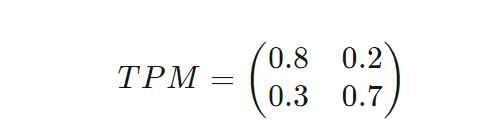
So, what I did was basically to Took this TPM(Transition Probability Matrix) to the power 4. My basis for doing this was this source-: https://www.math.pku.edu.cn/teachers/xirb/Courses/biostatistics/Biostatistics2016/Lecture4.pdf

So what I got was-:

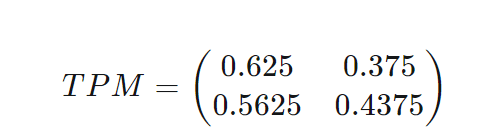
Now I am assuming that the rows means FROM and column side means TO. And the first element of row and column is "Coke". So, to find from Pepsi to Coke, I'd go to second row and first column, the value would be 0.5625

But the problem is that, I've conflicting source which claims the answer is sth else-:

It solves it like this-:

P=TPM

p=Current distribution=[0 1]

Now, for 2nd purchase

p²=p*P=[0.3 0.7]

For 3rd purchase-:
p³=p² * P
=[0.45 0.55]

For 4th purchase-:

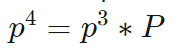
=[0.525 0.475]

Thus, it concludes that the required answer is 0.525.

Which one is correct in your opinion?

 

[pbuk]

The two methods are identical, although the notation is apalling: who in their right mind uses superscript for indexation in this context? Do they use subscript for exponentiation?

The difference arises entirely from the interpretation of the question:

Find the probability of using coke for a current pepsi user in 4th purchase?

Does this mean $p_0 = (0, 1)$ or $p_1 = (0, 1)$ ? You interpret that as the former, and I agree with you, however the alternative solution has assumed the latter so what they are calling $p^4 (!)$ is your $p_3$.

 

[shivajikobardan]

The two methods are identical, although the notation is apalling: who in their right mind uses superscript for indexation in this context? Do they use subscript for exponentiation?

The difference arises entirely from the interpretation of the question:

Does this mean $p_0 = (0, 1)$ or $p_1 = (0, 1)$ ? You interpret that as the former, and I agree with you, however the alternative solution has assumed the latter so what they are calling $p^4 (!)$ is your $p_3$.

The second TPM made by me was $TPM^4$
I am assuming that the rows are FROM and columns are TO
i.e row1, column1 is FROM Coke TO Coke i.e a coke eating guy again purchase coke.
But you're right. I've not seen a single textbooks about these examples so I'm also not sure why it's like that. I just tried to understand that pdf and solved accordingly.

 

[FactChecker]

I interpreted the question as you did, but as @pbuk points out, the book answer assumes that "a current pepsi user" implies that the first purchase was a pepsi. Therefore, it is asking for the probability after another 3 purchases. I think the book may be correct.
The important point is that your approach is correct. It is just a matter of being very careful of the problem statement.

 

[pbuk]

I've not seen a single textbooks about these examples

I've linked these excellent course notes a number of times here, perhaps it ought to be a FAQ: http://www.statslab.cam.ac.uk/~rrw1/markov/index.html