Ranku
- 433
- 18
What are the non-gravitational ways of determining mass of galaxies, and how accurate are they?
What do you say about non-gravitational methods like X-ray emission or the Sunyaev-Zel'dovich effect - aren't they adequate or accurate enough?Drakkith said:There aren't any to my knowledge. We can't even determine the mass of the planets in the solar system without using gravity. Heck, even scales to measure weight (which is converted into a mass) depend on gravity for the most part. Without gravity you are probably stuck with applying a force and measuring the acceleration of an object, which is extremely impractical for objects on Earth and downright impossible for essentially every astronomical object. Even something like a redshift measurement is using gravity.
I confess that I am not familiar with those techniques.Ranku said:What do you say about non-gravitational methods like X-ray emission or the Sunyaev-Zel'dovich effect - aren't they adequate or accurate enough?
Knowing what one doesn't know is also knowing.Drakkith said:I confess that I am not familiar with those techniques.
Precision In AstronomyRanku said:What are the non-gravitational ways of determining mass of galaxies, and how accurate are they?
For elliptical galaxies the width of the absorption lines from all of the stars blended together is used to measure the mass of elliptical galaxies. The width of the absorption lines depends on the spread of the distribution of the velocities---the velocity dispersion. The elliptical galaxy's mass = k × (velocity dispersion)2 × (the distance the stars are from the galaxy center)/G, where k is a factor that depends on the shape of the galaxy and the angle the galaxy is from Earth.
[Karl] Gebhardt compare[d] the mass of each black hole with the average velocities of the billion-or-so stars that surround each hole out to a distance of several thousand light-years. This swarm of stars—a major component of a galaxy—is known as the bulge, and the stellar velocities provide a measure of the bulge's mass.
When Gebhardt made the comparison, he was stunned. Regardless of their size, the bulges always turned out to be 500 times as massive as the giant black holes at the hub of their galaxies.
Do you find it surprising that there should be a tight relation between stellar mass or baryonic mass and total inferred mass (including dark matter), given that dark matter is 'different' from matter?ohwilleke said:Precision In Astronomy
It is important to recognize that, in general, astronomer's measurements of galaxy masses (outside some special cases like our own Milky Way galaxy) aren't terribly precise by the standards of other disciplines of physics.
In astronomy, the common unit of relative error is the "dex" with 0.5 dex, for example, (which looks nice and small in print) meaning 100.5 times or divided by the best fit estimate of the value, which is ± 316% (which looks grossly and embarrassing large in print). So if the best fit value is 1 and the error is 0.5 dex, then the plus or minus one standard deviation expected value of the quantity is from about 0.316 to 3.16.
Astronomy measurements to 0.1 dex precision (± 125%) is usually considered quite good, and mere order of magnitude precision (i.e. 1 dex uncertainties such as 0.1 to 10 for a best fit value of 1) is pretty much par for the course for distant galaxies.
How do you define the mass of a galaxy?
The Implied Dark Matter Particle Assumption And General Relativistic Considerations
Usually galaxy mass is defined based upon the gravitational pull on an external observer in the near vicinity of the galaxy with the assumption of approximately Newtonian gravity, whether or not this gravitational field is actually due in part to dark matter, or is actually in part to non-linear modifications of Newtonian gravity that don't actually involved dark matter particles.
But, there are other ways that you could define galaxy mass, which due to general relativity, is intrinsically observer location dependent and also depends upon the geometry of the massive objects within the galaxy relative to each other. In general relativity, the mass of a galaxy is not, at a fundamental level, a simple scalar quantity that is not dependent upon which is observing it or how the stuff in a galaxy is arranged.
In general, in general relativity, the mass of a system of massive objects that are close to each other as measured the gravitational pull of the system as a whole on observers outside the system, will be greater than the sum of the masses of the components of the system would if they were isolated from each other by distances so great that they have negligible gravitational pulls on each other.
In most galaxy scale applications this effect is presumed to be negligible, but we know from general relativity that it isn't zero.
If you defined galaxy mass as the sum of the masses of the individual stars and dark matter particles in the galaxy if they had been separated from each other at infinite distances, the galaxy mass would be a bit lower than the mass of the galaxy treated as a single composite system.
Practically, this difference might not matter much, but there is something to be said for conceptual clarity in your definitions, when this is possible.
What Masses Are Included In The Galaxy You Weigh?
Another definitional issue is to decide where the galaxy starts and stops.
Knowing where a galaxy starts and stops is harder than it sounds, because we observe light from the galaxy with a minimum luminosity threshold of observation with our "telescopes" (put in scare quotes to make clear that I mean all astronomy observation devices and not just conventional visible light telescopes that we think of in a strict sense as telescopes). But the density of stars in a galaxy generically gets lower as you move away from its center and there will necessarily be some stars at the fringes of a galaxy that are still in the gravitational pull of a galaxy but can't be observed because the fringe of the galaxy is too dim.
The further away a galaxy is, as measured by parallax if it is very close to the solar system, or by redshift, if it is further away from the solar system, the less of the fringe of a galaxy you can see. So if you want to compare high redshift galaxy masses to low redshift galaxy masses, you need to either account for this systemic bias towards underestimating the mass of distant galaxies statistically, or by using a restrictive definition of what counts as the galaxy's mass that minimizes the impact of this systemic error within the range of redshifts in your sample (or by using methods to "weigh" distant galaxies that are insensitive to this effect).
For example, one might measure all of the mass within X parsecs of the center of the galaxy. There are several common definitions of what counts as mass that is part of the galaxy that are commonly used. Most of these operational definitions of a galaxy's mass are somewhat arbitrary in contrast to more "natural" definitions of what is part of a galaxy, in order to assure greater consistency when using "telescopes" of limited accuracy, especially at the fringes of a galaxy.
It also matters, for example, if your definition of the mass of a galaxy does or does not include its satellite galaxies and globular clusters that are gravitationally bound to a galaxy.
Many kinds of galaxies have mass distributions with "long tails" so deciding where to put the cutoff point for measuring a galaxy's mass matters quite a bit.
This also means that converting measurements from one kind of measurement (e.g. gravitational lensing of light near a galaxy that implicitly is measuring a very global and comprehensive measure of a galaxy's mass) to measurements from another kind of measurement (e.g. luminous matter based) where an X parsec from the center definition excluding satellite galaxies and globular clusters definition might be more natural, is a non-trivial matter. To convert from a less arbitrary definition to a more arbitrary definition or visa versa, you need to make assumptions about the overall mass distribution of the galaxies you are converting the mass of from one definition to another.
Of course, if you are comparing the masses of lots of different galaxies for some reason, you would like to use consistent definitions for your measurements.
What counts as a non-gravitational method?
This depends upon what you mean by "non-gravitational ways" which is entirely unclear as other posts in this thread have noted.
Some of the more common ways to measure galaxy mass are summarized here. The list of methods considered below isn't exhaustive, but one has to start somewhere. If you had other methods in mind, the precision of those could be considered as well.
Various Methods Of Weighing Galaxies Considered
The most direct gravitational way to determine the mass of galaxies is with gravitational lensing of light around the galaxy. This is quite precise (depending upon your "telescope" and how far away the galaxy is), but not available for all galaxies. You need a light source behind the galaxy from the perspective of a solar system observer whose bend can be determined to do that, and this isn't always feasible.
The stellar mass in a galaxy can be estimated from the light generated by the galaxy and there is a tight empirical relationship between the stellar mass of a galaxy and its total inferred mass including dark matter phenomena.
This relationship is even more tight is you can make a reasonable estimate based upon galaxy type of the amount of non-stellar ordinary matter (e.g. elemental hydrogen in empty space) which is present in the galaxy, to get the total amount of ordinary "baryonic matter" in a galaxy. This empirical relationship is roughly as tight as the limits of telescope precision in estimating stellar mass from luminosity. This precision is generally speaking greater for a given level of "telescope" power when galaxies are closer to us and less precise for more distant galaxies.
The dynamics of the galaxy (e.g., a rotationally supported spiral galaxy's rotation speed) can be used to quite accurately estimate its mass through a known scaling relationship between mass and rotation speed that flows from the gravitational relationships between the stuff in a galaxy. This isn't quite as precise as the estimate based upon baryonic mass, but it's close (maybe 0.1-0.2 dex less precise).
The accuracy of mass estimates based upon rotational speed depends a great deal on the angle of inclination between a solar system bound observer and the galaxy. A galaxy which is edge on, or has a hard to determine angle of inclination is harder to "weigh" accurately with this method than a galaxy which is face on or has an easy to determine angle of inclination. Uncertainty in the angle of inclination is often the dominant source of uncertainty in the overall measurement of the mass of the galaxy in these cases.
(Source)
If you can estimate the size of the supermassive black hole at the center of a galaxy by some means, there is a scaling relationship between the mass of the black hole and the mass of the galaxy, although it isn't as tight as the relationship between baryonic (i.e. ordinary matter) mass and inferred total mass including inferred dark matter.
If you have a galaxy and satellite galaxies, or a couple of galaxies close to each other, and you know the mass of one, you can estimate the mass of the others from the dynamics of the neighboring galaxies which is basically gravitational, but not quite as direct.
More crudely, if two galaxies of the same type have similar red-shifts and luminosity and the mass of one is known, you could simply assume that the other is of comparable mass adjusting linearly for luminosity.
Post #3 in this thread mentions "non-gravitational methods like X-ray emission or the Sunyaev-Zel'dovich effect" which aren't the most precise measurements available but "good enough for government work" in many circumstances and probably more precise than estimates based upon supermassive black hole mass.
Generically, stuff, such as interstellar dust or objects that strongly lens light already gravitationally lensed by the galaxy you want to weigh, between the solar system and the galaxy observed can impair the precision of a galaxy mass measurement because it degrades the quality of the observations used to make the measurement.
Similarly, generically, the further away from us a galaxy is, the less precise our measurement of its mass will be, because our image of it has lower resolution relative to the size of the galaxy. At closer distances, rotation speed or velocity dispersion might be more viable, while at immense distances with very early galaxies, total luminosity might be the only thing we can measure.
Also, sometimes we can measure average galaxy size at a given redshift and direction of observation, but not the size of a particular individual galaxies, for example, by using cosmic microwave background radiation patterns to estimate average galaxy size.
It is very surprising in a dark matter particle hypothesis for dark matter phenomena. There should be some general relationship but there is no good reason that it should be so tight, particularly when the overall percentage of inferred dark matter in galaxies varies greatly (it wouldn't be nearly as surprising if the percentage of dark matter was the same in every galaxy). The percentage of inferred dark matter also varies systemically with the size and shape of a galaxy, and there is no good explanation in a dark matter particle hypothesis for the observed systemic variations seen.Ranku said:Do you find it surprising that there should be a tight relation between stellar mass or baryonic mass and total inferred mass (including dark matter), given that dark matter is 'different' from matter?
Could you suggest some papers that show how dark matter varies between galaxies?ohwilleke said:There should be some general relationship but there is no good reason that it should be so tight, particularly when the overall percentage of inferred dark matter in galaxies varies greatly (it wouldn't be nearly as surprising if the percentage of dark matter was the same in every galaxy). The percentage of inferred dark matter also varies systemically with the size and shape of a galaxy, and there is no good explanation in a dark matter particle hypothesis for the observed systemic variations seen.
What Kinds of Galaxies Exist?Ranku said:Could you suggest some papers that show how dark matter varies between galaxies?
Astronomers have known since the 1920s that the modern-day universe consists mainly of two galaxy types—young-looking, disk-shaped spirals like the Milky Way, and elderly, football-shaped ellipticals. Ellipticals have a reddish tinge—an indication that they are old and finished forming stars long ago—while spirals have a bluish tinge, a sign of recent star formation.
A few years ago, researchers found that in the universe today, these two populations divide sharply by weight. An analysis of the Sloan Digital Sky Survey, which has recorded about 1 million nearby galaxies of the northern sky, revealed that the "red and dead" ellipticals nearly always tip the scales at masses greater than the Milky Way, while the star-forming spirals fall below that weight. Somehow, star birth was systematically and dramatically quenched in the big guys but proceeded unimpeded in the spiral small-fry.
The puzzle deepened in 2005 when Sandy Faber of the University of California, Santa Cruz, and her colleagues announced that they found the same galactic dichotomy when the universe was 7 billion years old, half its current age.
(Source for quote above. A kiloparsec is about 3,262 light years. M⊙ is the mass of our Sun.)Most galaxies have a total mass between ~ 107 M⊙ and 1012 M⊙. They range in size from a few kiloparsecs, to over one hundred kiloparsecs in diameter. Our own Milky Way contains over 100 billion stars, including our Sun, and the stellar disk extends to about 50 kpc in diameter. The spherical stellar halo extends up to 100 kpc. . . . Galaxies are classified according to how they appear . . . the most common classification scheme in use today is the Hubble classification scheme. Galaxies can be classified into the following broad categories, although there are many sub-catagories within each classification:
- Elliptical,
- Spiral,
- Irregular, and
- Dwarf galaxies.
A lenticular galaxy (denoted S0) is a type of galaxy intermediate between an elliptical (denoted E) and a spiral galaxy in galaxy morphological classification schemes. It contains a large-scale disc but does not have large-scale spiral arms. Lenticular galaxies are disc galaxies that have used up or lost most of their interstellar matter and therefore have very little ongoing star formation. They may, however, retain significant dust in their disks. As a result, they consist mainly of aging stars (like elliptical galaxies). Despite the morphological differences, lenticular and elliptical galaxies share common properties like spectral features and scaling relations. Both can be considered early-type galaxies that are passively evolving, at least in the local part of the Universe.
We make an inventory of the baryonic and gravitating mass in structures ranging from the smallest galaxies to rich clusters of galaxies. We find that the fraction of baryons converted to stars reaches a maximum between M500 = 1E12 and 1E13 Msun, suggesting that star formation is most efficient in bright galaxies in groups. The fraction of baryons detected in all forms deviates monotonically from the cosmic baryon fraction as a function of mass. On the largest scales of clusters, most of the expected baryons are detected, while in the smallest dwarf galaxies, fewer than 1% are detected. Where these missing baryons reside is unclear.
[A]t equal luminosity, flattened medium-size elliptical galaxies are on average five times heavier than rounder ones, and . . . the non-baryonic matter content of medium-size round galaxies is small.
MOND is mathematically equivalent to the baryonic Tully-Fischer relation, and that phenomenological scaling rule is a very good fit to the data. As explained in the articles below, dark matter particle theories struggle greatly to reproduce the baryonic Tully-Fischer relation which is observed in Nature.Ranku said:Also, any of the papers that clearly demonstrates MOND performs better with Tully-Fisher relation?
S. Pradyumna, Shantanu Desai, "A test of Radial Acceleration Relation for the Giles et al Chandra cluster sample" arXiv:2107.05845 33 Physics of the Dark Universe 100854 (July 13, 2021). DOI: 10.1016/j.dark.2021.100854We carry out a test of the radial acceleration relation (RAR) for a sample of 10 dynamically relaxed and cool-core galaxy clusters imaged by the Chandra X-ray telescope, which was studied in Giles et al. For this sample, we observe that the best-fit RAR shows a very tight residual scatter equal to 0.09 dex. We obtain an acceleration scale of 1.59×10^−9m/s^2, which is about an order of magnitude higher than that obtained for galaxies. Furthermore, the best-fit RAR parameters differ from those estimated from some of the previously analyzed cluster samples, which indicates that the acceleration scale found from the RAR could be of an emergent nature, instead of a fundamental universal scale.
Paolo Salucci and Nicola Turini, "Evidences for Collisional Dark Matter In Galaxies?" (July 4, 2017).The more we go deep into the knowledge of the dark component which embeds the stellar component of galaxies, the more we realize the profound interconnection between them. We show that the scaling laws among the structural properties of the dark and luminous matter in galaxies are too complex to derive from two inert components that just share the same gravitational field. In this paper we review the 30 years old paradigm of collisionless dark matter in galaxies. We found that their dynamical properties show strong indications that the dark and luminous components have interacted in a more direct way over a Hubble Time. The proofs for this are the presence of central cored regions with constant DM density in which their size is related with the disk length scales. Moreover we find that the quantity ρDM(r,L,RD)ρ⋆(r,L,RD) shows, in all objects, peculiarities very hardly explained in a collisionless DM scenario.
Paolo Salucci, "The distribution of dark matter in galaxies" (November 21, 2018) (60 pages, 28 Figures ~220 refs. Invited review for The Astronomy and Astrophysics Review).The distribution of the non-luminous matter in galaxies of different luminosity and Hubble type is much more than a proof of the existence of dark particles governing the structures of the Universe. Here, we will review the complex but well-ordered scenario of the properties of the dark halos also in relation with those of the baryonic components they host. Moreover, we will present a number of tight and unexpected correlations between selected properties of the dark and the luminous matter. Such entanglement evolves across the varying properties of the luminous component and it seems to unequivocally lead to a dark particle able to interact with the Standard Model particles over cosmological times. This review will also focus on whether we need a paradigm shift, from pure collisionless dark particles emerging from "first principles", to particles that we can discover only by looking to how they have designed the structure of the galaxies.
Paolo Salucci, Nicola Turini, Chiara Di Paolo, "Paradigms and Scenarios for the Dark Matter Phenomenon" arXiv:2008.04052 (August 10, 2020).Well known scaling laws among the structural properties of the dark and the luminous matter in disc systems are too complex to be arisen by two inert components that just share the same gravitational field. This brings us to critically focus on the 30-year-old paradigm, that, resting on a priori knowledge of the nature of Dark Matter (DM), has led us to a restricted number of scenarios, especially favouring the collisionless Λ Cold Dark Matter one. Motivated by such observational evidence, we propose to resolve the dark matter mystery by following a new Paradigm: the nature of DM must be guessed/derived by deeply analyzing the properties of the dark and luminous mass distribution at galactic scales. The immediate application of this paradigm leads us to propose the existence of a direct interaction between Dark and Standard Model particles, which has finely shaped the inner regions of galaxies.
Lin Wang, Da-Ming Chen, Ran Li "The total density profile of DM halos fitted from strong lensing" (July 31, 2017). As the body text of this paper explains:We find that, at outer parts for a typical galaxy, the rotation curve calculated with our fitted density profile is much lower than observations and those based on simulations, including the NFW profile. This again verifies and strengthen the conclusions in our previous works: in ΛCDM paradigm, it is difficult to reconcile the contradictions between the observations for rotation curves and strong gravitational lensing.
It is now well established that, whatever the manners the baryon effects are included in the collisionless CDM N-body cosmological simulations, if the resultant density profiles can match the observations of rotation curves, they cannot simultaneously predict the observations of strong gravitational lensing (under- or over-predict). And for the case of typical galaxies, the reverse is also true, namely, the SIS profile preferred by strong lensing cannot be supported by the observations of rotation curves near the centers of galaxies.
L.V. Sales, et al., "The low-mass end of the baryonic Tully-Fisher relation" (February 5, 2016). This paper manages to simulate the Tully-Fisher relation only with a model that has sixteen parameters carefully "calibrated to match the observed galaxy stellar mass function and the sizes of galaxies at z = 0" and "chosen to resemble the surroundings of the Local Group of Galaxies", however, and still struggles to reproduce the one parameter fits of the MOND toy-model from three decades ago. Any data set can be described by almost any model so long as it has enough adjustable parameters.[T]he literature is littered with failed attempts to reproduce the Tully-Fisher relation in a cold dark matter-dominated universe. Direct galaxy formation simulations, for example, have for many years consistently produced galaxies so massive and compact that their rotation curves were steeply declining and, generally, a poor match to observation. Even semi-analytic models, where galaxy masses and sizes can be adjusted to match observation, have had difficulty reproducing the Tully-Fisher relation, typically predicting velocities at given mass that are significantly higher than observed unless somewhat arbitrary adjustments are made to the response of the dark halo.
P.L. Biermann, H.J. de Vega, N.G. Sanchez, "Highlights and Conclusions of the Chalonge Meudon workshop 2012: warm dark matter galaxy formation in agreement with observations" arXiv:1305.7452v2 (June 26, 2013) (from the body text at https://arxiv.org/pdf/1305.7452v2.pdf).Evidence that Cold Dark Matter (ΛCDM), CDM+ baryons and its proposed tailored cures do not work in galaxies is staggering, and the CDM wimps (DM particles heavier than 1 GeV) are strongly disfavoured combining theory with galaxy astronomical observations.
Isabel M.E. Santos-Santos, et al., "Baryonic clues to the puzzling diversity of dwarf galaxy rotation curves" (November 20, 2019).Dwarf galaxy rotation curves are challenging to reproduce in the standard Lambda Cold Dark Matter (LCDM) cosmogony. In some galaxies, rotation speeds rise rapidly to their maximum value, consistent with the circular velocity curves expected of cuspy LCDM halos. In others, however, rotation speeds rise more slowly, revealing large “inner mass deficits” or “cores” when compared with LCDM halos (e.g., de Blok 2010). This diversity is unexpected in LCDM, where, in the absence of modifications by baryons, circular velocity curves are expected to be simple, self-similar functions of the total halo mass (Navarro et al. 1996b, 1997; Oman et al. 2015). . . . the relation between baryon surface density and rotation curve shape is quite weak in the dwarf galaxy regime, and thus unlikely to drive the diversity. . . . Our results do show, in agreement with earlier work, that SIDM leads to a wide distribution of rotation curve shapes. However they also highlight the fact that outliers, be they large cores or cuspy systems, are not readily accounted for in this scenario, an issue that was also raised by Creasey et al. (2017). Whether this is a critical flaw of the SIDM scenario, or just signals the need for further elaboration, is still unclear.We end by noting that the rather peculiar relation between inner baryon dominance and rotation curve shapes could be naturally explained if non-circular motions were a driving cause of the diversity. For this scenario to succeed, however, it would need to explain why such motions affect solely low surface brightness galaxies, the systems where the evidence for “cores” is most compelling. . . . Until then, we would argue that the dwarf galaxy rotation curve diversity problem remains, for the time being, open.
(Source for image). The fall off outliers in the super spirals may be related to an issue related to how the rotation velocity should be measured in these galaxies.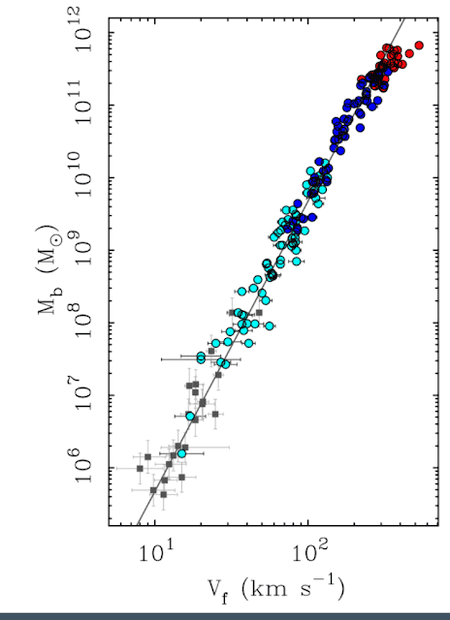
Thanks. Look forward to it.ohwilleke said:I can. I'll track down some citations when I get a chance.
Done.Ranku said:Thanks. Look forward to it.
Thank you so much. Will go through it and see what questions come upohwilleke said:Done.