Mass pushed upward a hill, calculate the coefficient of friction.

[b_andries]

Hi!

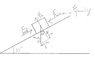
A block with mass 35 kg is pushed upward with a horizontal force of 400N along a slope at an angle of 30 °. The block makes a displacement of 2 meters, where it's speed changes from 1m/s to 1,8m/s. What is the Coefficients Of Friction?

1) 0.312

2) 1.099

3) 0.039

4) 1.31


my attempt here for this problem is:

m.g.µ + m.g sin 30° - 400 / cos 30° = m.a

I calculated the acceleration which is 0,56
so

35 . 9,81 . µ + 35.9,81 sin 30° - 400 / cos 30° = 35.0,56
If i then calculate µ i get 0,90 which is not an answer possibility.
What am i doing wrong here?

Thanks in advance!

 

[da_nang]

m.g.µ + m.g sin 30° - 400 / cos 30° = m.a

Hi!
You've set up the free-body diagram wrong. Start filling in forces with known magnitudes, gravity, friction and the pushing force. Then start playing with the other unknown ones.

Just so you know, the formula for friction is $$F_{\mu} = \mu N$$ In this case, there's more than one force affecting the normal force. Can you guess which one?

 

[tiny-tim]

hi b_andries!

you don't need the acceleration …

just use the work energy theorem (change in KE and PE = work done )

(but of course you still need da_nang's hint about the normal force)

 

[b_andries]

Hi!
You've set up the free-body diagram wrong. Start filling in forces with known magnitudes, gravity, friction and the pushing force. Then start playing with the other unknown ones.

Just so you know, the formula for friction is $$F_{\mu} = \mu N$$ In this case, there's more than one force affecting the normal force. Can you guess which one?

Fpush - (Ffriction + Fgravity) = m . a
400/cos30° - 343 cos 30° µ - 343 sin 30° = 35 . 0,56
µ = 0,91

I find only 1 Force affecting the normal force that is mg cos30°

 

[b_andries]

hi b_andries!

you don't need the acceleration …

just use the work energy theorem (change in KE and PE = work done )

(but of course you still need da_nang's hint about the normal force)

0,5 . 35 1² + 0 = 0,5 . 35 1,8² + 35.9,81.2

The change in KE and PE is = 726J
726J = F.x
F= 726/2 = 363N

And then I'm stuck because I don't see any second force affection the normal force :S

 

[tiny-tim]

hi b_andries!

… I don't see any second force affection the normal force :S

ohhhh i see why …

your diagram is wrong …

your F_push should be horizontal

try again! ​

 

[b_andries]

hi b_andries!


ohhhh i see why …

your diagram is wrong …

your F_push should be horizontal

try again! ​

The horizontal force is 400 but than the horizontal upward force must be 400/cos30° no?

 

[tiny-tim]

The horizontal force is 400 but than the horizontal upward force must be 400/cos30° no?

but that's larger!

and you need to recalculate the normal force

draw a new diagram and start again! ​

 

[b_andries]

Aha i think i got it
Fpush should be Fcos30° instead of F/cos30°
And the horizontal force should add up to the normal force!

 

[b_andries]

So the upward force is 400cos30°
The normal force is = mgcos30° + 400sin30°

So than my equation becomes =

400 cos 30° - (343 cos30° + 400 sin30°).µ - 343 sin 30° = 35.0,56

right?

than µ = 0,312