- #1
Cdh0127
- 3
- 0
ηϖ1. Homework Statement
I=½MR2
PE=mgh
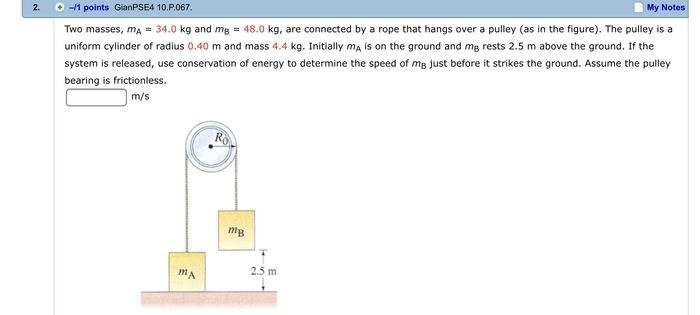
The first thing that jumped out at me was "uniform cylinder" so I went ahead and calculated the moment of inertia for the cylinder and got I=½(4.4)(.4)2 = .352 and held onto that.
Then, I calculated the forces due to gravity of each mass that is pulling down on the string.
Fmb = 48kg×9.8m/s2 = 470.4N
I'm not sure if I do the same for ma because it's resting on the table, so is there a force pulling on the string creating tension?
But the next thing I did was find the gravitational potential energy of mb:
PE = mgh = 48kg×9.8m/s2×2.5m = 1176 J.
I'm not sure if torque is needed, but I went ahead and calculated it anyways:
T=F×r = 470.4N×.4m = 188.16
And that is all I can think to do. I'm not sure how the radius, inertia, mass, and other properties of the pulley affect the masses A and B that move up and down via the string over that pulley.
Could I take the 1176 J of potential energy and set it equal to ½mv2? But what mass would I use? Mass of the system (A + B)? Solve for V? That seems too simple for this section, because we are learning about angular kinematics, torque...etc. I think I'm missing something.
Thank you for your time and advice!
Homework Equations
I=½MR2
PE=mgh
The Attempt at a Solution
The first thing that jumped out at me was "uniform cylinder" so I went ahead and calculated the moment of inertia for the cylinder and got I=½(4.4)(.4)2 = .352 and held onto that.
Then, I calculated the forces due to gravity of each mass that is pulling down on the string.
Fmb = 48kg×9.8m/s2 = 470.4N
I'm not sure if I do the same for ma because it's resting on the table, so is there a force pulling on the string creating tension?
But the next thing I did was find the gravitational potential energy of mb:
PE = mgh = 48kg×9.8m/s2×2.5m = 1176 J.
I'm not sure if torque is needed, but I went ahead and calculated it anyways:
T=F×r = 470.4N×.4m = 188.16
And that is all I can think to do. I'm not sure how the radius, inertia, mass, and other properties of the pulley affect the masses A and B that move up and down via the string over that pulley.
Could I take the 1176 J of potential energy and set it equal to ½mv2? But what mass would I use? Mass of the system (A + B)? Solve for V? That seems too simple for this section, because we are learning about angular kinematics, torque...etc. I think I'm missing something.
Thank you for your time and advice!