lenilein
- 3
- 2
- TL;DR
- Massflow of steam to be supplied to a drying cylinder
Good afternoon,
I am trying to calculate the massflow of steam required in a cylinder used for paper drying but I think there is a bug in my calculation and I would love to get your help to find where the issue is!
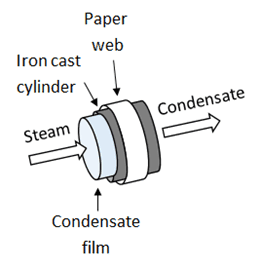
A condensate layer along the cylinder inner surface and the cylinder shell separate the steam from the paper placed on the cylinder and the overall heat transfer coefficient is determined as:
U=1 / (1 / U condensate + 1 / U cylinder)
where H is the known heat transfer coefficient of the condensate, and since the cylinder has a large diameter:
U cylinder (W/m2.K) = thermal conductivity cylinder (W/m.K) / thickness cylinder shell (m)
The temperature of the paper web is calculated using an energy balance on the paper (taking into account the energy flow from steam to paper and convective heat transfer between the paper and the surrounding air)
According to physical laws of heat transfer:
Heat transferred from steam to paper (in Watt) = Area heat transfer (in m2) * U (in W/m2.K) * (T steam - T paper)
Which means that if the thermal conductivity of the cylinder shell is higher and other parameter values remain same, the resulting heat flow from steam to paper will be higher.
Now comes the tricky part: I am calculating the massflow of steam required in the cylinder as follows:
Massflow steam (kg/s) = 0.001 * Heat transferred from steam to paper (W) / Enthalpy of steam condensation (in kJ/kg)
However, this means that for a higher thermal conductivity of the shell the massflow of steam required will be higher => from my understanding this shouldn’t be the case since improved heat transfer should lead to steam savings.
Is my formula for the steam massflow maybe wrong?
Many many thanks in advance!
I am trying to calculate the massflow of steam required in a cylinder used for paper drying but I think there is a bug in my calculation and I would love to get your help to find where the issue is!
Saturated steam is continuously supplied to a cylinder. The steam condenses in the cylinder and the condensate is continuously removed from the cylinder as represented here:A condensate layer along the cylinder inner surface and the cylinder shell separate the steam from the paper placed on the cylinder and the overall heat transfer coefficient is determined as:
U=1 / (1 / U condensate + 1 / U cylinder)
where H is the known heat transfer coefficient of the condensate, and since the cylinder has a large diameter:
U cylinder (W/m2.K) = thermal conductivity cylinder (W/m.K) / thickness cylinder shell (m)
The temperature of the paper web is calculated using an energy balance on the paper (taking into account the energy flow from steam to paper and convective heat transfer between the paper and the surrounding air)
According to physical laws of heat transfer:
Heat transferred from steam to paper (in Watt) = Area heat transfer (in m2) * U (in W/m2.K) * (T steam - T paper)
Which means that if the thermal conductivity of the cylinder shell is higher and other parameter values remain same, the resulting heat flow from steam to paper will be higher.
Now comes the tricky part: I am calculating the massflow of steam required in the cylinder as follows:
Massflow steam (kg/s) = 0.001 * Heat transferred from steam to paper (W) / Enthalpy of steam condensation (in kJ/kg)
However, this means that for a higher thermal conductivity of the shell the massflow of steam required will be higher => from my understanding this shouldn’t be the case since improved heat transfer should lead to steam savings.
Is my formula for the steam massflow maybe wrong?
Many many thanks in advance!
Last edited:
 !
!