Massive rotating drum on bearings with friction

[erore]

I came across the following example. I have a mass $m'$ that is suspended from a massless rope which is wound around a drum of mass $m$. The radius of the drum is $R$. The drum is fixed on a shaft with bearings of radius $r$. I am supposed to determine coefficient of friction between the bearings and the drum but for now I am stuck with the forces diagram.
I created something like that:

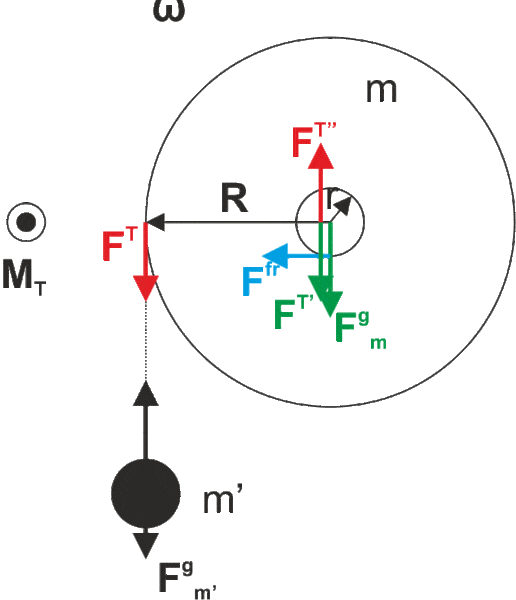
In my solution I add a pair of forces of the same magnitude and opposite direction $F^{T''}$ and $F^{T'}$. $F^{T''}$ and $F^{T}$ make a force couple which generates some momentum about the axis of the drum (which contributes to rotation motion). However, $F^{T'}$ acts on the center of mass of the drum and adds up with gravitation force. Thus, the resulting force exerted by the drum on the bearing is bigger than if there was no $m'$. Consequently the friction is bigger too.

My question is whether this is correct. The solution I have only calculates the torque due to $m'$ and does not introduce the force couple therefore it does not have the additional force on the center of mass and consequentially no additional item in the normal force and friction respectively.

I am also curious, the friction itself produces a torque, if my reasoning above is correct, it would create another force couple, giving rise yet to another force acting on the center of mass of the drum which could go on and on. This is confusing for me at the moment.

 

[mfb]

Friction between what and what? Is the drum attached to something or in contact with something? That will somehow balance the force F^T (otherwise the whole setup accelerates downwards).

 

[erore]

I am sorry, the first paragraph was nonsense. I corrected. Basically, there is a hole in the middle of the drum of radius r and a shaft with bearings is inserted into that hole. The friction I mention is between the inner hole of the drum and the bearings.

 

[mfb]

Ah. I think I would draw the friction force at the upper side and in the other direction.
Afterwards, I would add variables for the angular acceleration and the force on the shaft and solve for those.

 

[PJC01]

I can confirm that your reasoning is correct. The additional force couple generated by F^{T''} and F^{T'} does indeed contribute to the overall torque on the drum and can affect the normal force and friction between the bearings and the drum. This is because the force couple creates a moment arm, which can increase the torque and therefore the friction force.

Additionally, the friction force itself can indeed create another force couple and contribute to the overall torque. This can create a feedback loop where the friction force increases the torque, which in turn increases the friction force, and so on. This is a common phenomenon in rotating systems and is known as self-excited vibration.

In order to accurately determine the coefficient of friction between the bearings and the drum, it is important to consider all of these forces and their effects on the system. Your approach of including the force couple in your force diagram is a valid and necessary step in understanding the dynamics of this system.