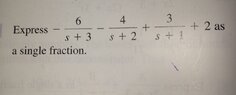Master Algebraic Fractions: Step-by-Step Guide with 3+ Sum Examples

[fordy2707]

hi all thanks for any help ,Can You solve:

View attachment 5445

I have the answer in my book but I don't know how the answer is reached

please show steps to solve, i can solve 2 sum fractions but not sure where to start with 3 or more sums involved

 

[MarkFL]

We are given the expression:

$$-\frac{6}{s+3}-\frac{4}{s+2}+\frac{3}{s+1}+2$$

And instructed to rewrite this expression as a single rational expression. Before we can do this, we need to determine the lowest common denominator (LCD), and since all denominators are prime with respect to each other, this will simply be the product of them all.

To make each term have this LCD, we need to take the LCD, and divide by denominator each term already has, and then multiply each term by 1 in the form of this quotient divided by itself. For example, the first term already has a denominator of $s+3$, and so we find the quotient:

$$\frac{(s+3)(s+2)(s+1)}{s+3}=(s+2)(s+1)$$

And so we will want to multiply the first term by:

$$1=\frac{(s+2)(s+1)}{(s+2)(s+1)}$$

I am emphasizing that this expression is equal to 1 so that it is clear that in doing so we are not changing the value of that term. Doing the same for the other terms, we will have:

$$-\frac{6}{s+3}\cdot\frac{(s+2)(s+1)}{(s+2)(s+1)}-\frac{4}{s+2}\cdot\frac{(s+3)(s+1)}{(s+3)(s+1)}+\frac{3}{s+1}\cdot\frac{(s+3)(s+2)}{(s+3)(s+2)}+2\cdot\frac{(s+3)(s+2)(s+1)}{(s+3)(s+2)(s+1)}$$

Now, all 4 terms have the same denominator, and we can combine them:

$$\frac{-6(s+2)(s+1)-4(s+3)(s+1)+3(s+3)(s+2)+2(s+3)(s+2)(s+1)}{(s+3)(s+2)(s+1)}$$

And so now we have done as instructed. You may wish to expand and then combine like terms in the numerator. :)

 

[fordy2707]

Nice one with your help I've worked it out, it's a long calculation to get the simplest form with no brackets but a good challenge

 

[suluclac]

All we're doing here is repeating a/b + c/d = (ad + bc)/bd. If you're used to doing this, this should be easy.