- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Mastering Moments | Cathy's Question Answered
- Thread starter CathyLou
- Start date
-
- Tags
- Moments
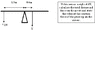
In summary: If so, what is the weight of the bar?On the 1st question, the clockwise moment would be 2.7 x 650 (1755N)... This would result in a force of 1140N. The weight of the bar would be 1140/650 which is 18.75kg.
Physics news on Phys.org
- #2
Hootenanny
Staff Emeritus
Science Advisor
Gold Member
- 9,622
- 9
Unfortunately there are not normally many mentors around at this time to approve your attachment, perhaps you could host your image on an external site, such as ImageShack?
- #3
CathyLou
- 173
- 1
Thanks for your suggestion.
Would it be okay though if I just sent the attatchment to you by a private message instead? It's just that I'm trying to not sign up to any more sites as I receive so much junk mail from sites that I used once or twice years ago.
Cathy
Would it be okay though if I just sent the attatchment to you by a private message instead? It's just that I'm trying to not sign up to any more sites as I receive so much junk mail from sites that I used once or twice years ago.
Cathy
- #4
Hootenanny
Staff Emeritus
Science Advisor
Gold Member
- 9,622
- 9
I believe that PM attachments also need mentor approval. However, I do know that ImageShack does not require you to sign up or any contact information. You can wait for a mentor to approve your attachment (which usually happens quickly when they're online), I just thought that you would get your question answered more rapidly this way.CathyLou said:Thanks for your suggestion.
Would it be okay though if I just sent the attatchment to you by a private message instead? It's just that I'm trying to not sign up to any more sites as I receive so much junk mail from sites that I used once or twice years ago.
Cathy
- #5
CathyLou
- 173
- 1
Okay. Thanks for replying. I'll take a look at ImageShack.
Cathy
Cathy
- #6
CathyLou
- 173
- 1
Ooh, that was quick!
Here's the link: http://img291.imageshack.us/img291/8981/question10fg0.th.gif
Thanks for the tip!
Cathy
Here's the link: http://img291.imageshack.us/img291/8981/question10fg0.th.gif
Thanks for the tip!
Cathy
Last edited by a moderator:
- #7
Hootenanny
Staff Emeritus
Science Advisor
Gold Member
- 9,622
- 9
No problem. I am assuming that the question requires an numerical answer. If this is the case, first you must find the force exerted at x. For this question one must assume that the seesaw is pivoted about its centre and the seesaw is in equilibrium.
Last edited:
- #8
CathyLou
- 173
- 1
Hootenanny said:No problem. I am assuming that the question requires an numerical answer. If this is the case, first you must find the force exerted at x. For this question one must assume that the seesaw is pivoted about its centre and the seesaw is in equilibrium.
Right, so the force at X is equal to 18N (anticlockwise moment = clockwise moment), but what do I do next to find the total downward force on the pivot, and then the reaction force? Would the total downward force be 7.2N + 18N?
Cathy
- #9
Astronuc
Staff Emeritus
Science Advisor
2023 Award
- 22,186
- 6,854
One would sum the applied downward forces AND the weight of the seesaw. If the pivot was off-centre, then one would have to determine the moments of the arms of the see-saw.Would the total downward force be 7.2N + 18N?
- #10
CathyLou
- 173
- 1
Astronuc said:One would sum the applied downward forces AND the weight of the seesaw. If the pivot was off-centre, then one would have to determine the moments of the arms of the see-saw.
Okay, thanks for your help.
Would I use trigonometry next to calculate the value of the reaction force of the pivot up on the seesaw?
Cathy
- #11
Hootenanny
Staff Emeritus
Science Advisor
Gold Member
- 9,622
- 9
Trigonometry is not necessary sum the forces as Astronuc says and then use the fact the the whole system is in equilibrium, in other words the upwards forces must be equal to the downwards forces.CathyLou said:Okay, thanks for your help.
Would I use trigonometry next to calculate the value of the reaction force of the pivot up on the seesaw?
Cathy
- #12
CathyLou
- 173
- 1
Hootenanny said:Trigonometry is not necessary sum the forces as Astronuc says and then use the fact the the whole system is in equilibrium, in other words the upwards forces must be equal to the downwards forces.
Oh, I get it now.
Thanks so much!
Cathy
- #13
Hootenanny
Staff Emeritus
Science Advisor
Gold Member
- 9,622
- 9
Twas a pleasure.CathyLou said:Oh, I get it now.
Thanks so much!
Cathy
- #14
CathyLou
- 173
- 1
I'd be really grateful if someone could please give some hints on how to do the next two questions as well.
Here's the link: http://img71.imageshack.us/img71/1157/questions14and15ge1.th.gif
Thank you.
Cathy
Here's the link: http://img71.imageshack.us/img71/1157/questions14and15ge1.th.gif
Thank you.
Cathy
Last edited by a moderator:
- #15
Hootenanny
Staff Emeritus
Science Advisor
Gold Member
- 9,622
- 9
Again, here you need to assume that the bars are in equilibrium (and are uniform), i.e. there is no net torque. The anti clockwise moments must equal the clockwise moments. Note that the weight of the bar will always act through it's centre of mass.
- #16
CathyLou
- 173
- 1
Hootenanny said:Again, here you need to assume that the bars are in equilibrium (and are uniform), i.e. there is no net torque. The anti clockwise moments must equal the clockwise moments. Note that the weight of the bar will always act through it's centre of mass.
Sorry to be a pain, but I still really don't get how to find the weight of the bar. Could you please give me an equation and then I'll put in the numbers from the question, as I've no idea what to do. I've looked over all my notes from class and I can't see anything that could help me with these questions.
Would the clockwise moment on the 1st question be 2.7 x 650 (1755N m)?
Thanks.
Cathy
- #17
rsk
- 289
- 260
Yes, and the moment of the weight is W x its distance from the pivot, which you know (centre of mass is the centre of a uniform beam, ie 1.5m from the end).
Equate the two moments, and you should get a value for W.
Equate the two moments, and you should get a value for W.
- #18
CathyLou
- 173
- 1
rsk said:Yes, and the moment of the weight is W x its distance from the pivot, which you know (centre of mass is the centre of a uniform beam, ie 1.5m from the end).
Equate the two moments, and you should get a value for W.
Thank you sooo much!
It was the centre of mass bit that I didn't realize. I get it now though - YAY!
Cathy
FAQ: Mastering Moments | Cathy's Question Answered
What is "Mastering Moments: A Step-by-Step Guide | Cathy's Question Answered"?
"Mastering Moments: A Step-by-Step Guide | Cathy's Question Answered" is a guidebook written by Cathy, a renowned expert in mastering moments and personal development. It provides a step-by-step approach to help individuals make the most out of their moments and achieve personal growth and fulfillment.
Who is Cathy and why is she qualified to write this guide?
Cathy is a scientist and a personal development coach with over 10 years of experience in the field. She has conducted extensive research on mastering moments and has helped numerous individuals achieve personal growth and success. Her expertise and knowledge make her highly qualified to write this guide.
How can "Mastering Moments" benefit me?
This guide can benefit you by providing a structured and practical approach to making the most out of your moments. It will help you understand the importance of being present and intentional in your actions and thoughts, and how this can lead to personal growth and fulfillment. It also offers tips and exercises to help you apply the concepts in your daily life.
Is "Mastering Moments" suitable for everyone?
Yes, "Mastering Moments" is suitable for anyone who wants to improve themselves and make the most out of their moments. It is a universal concept that can benefit people from all walks of life, regardless of age, gender, or background.
Can I use "Mastering Moments" in combination with other personal development techniques?
Absolutely! "Mastering Moments" can complement other personal development techniques and practices. In fact, it can enhance the effectiveness of other techniques by helping you be more present and intentional in your actions and thoughts. It can also be used as a standalone guide for personal growth and fulfillment.
Similar threads
- Replies
- 6
- Views
- 500
- Replies
- 2
- Views
- 1K
- Replies
- 27
- Views
- 2K
- Replies
- 6
- Views
- 2K
- Replies
- 4
- Views
- 1K
- Replies
- 25
- Views
- 1K
- Replies
- 7
- Views
- 1K
- Replies
- 4
- Views
- 506
- Replies
- 2
- Views
- 1K
- Replies
- 1
- Views
- 848
Share: