Mastering Tricky Trigonometric Integrals: Tips and Techniques for Success

[reaper616]

Hi. I'm having troubles calculating this indefinite integral. I have tried a few things, but none seem to work.

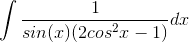
Actually, universal substitution does make it possible to integrate, but there has to be some shorter, more elegant way. Anyone?

 

[Count Iblis]

Replacing the 1 in the numerator by sin^2(x) + cos^2(x) does seem to work. You then do get the original integral back, but it is multiplied by 1/2 so you can move it back to the left hand side to solve for it.

 

[reaper616]

Replacing the 1 in the numerator by sin^2(x) + cos^2(x) does seem to work. You then do get the original integral back, but it is multiplied by 1/2 so you can move it back to the left hand side to solve for it.

I'm sorry, but I'm not sure that I understand what are you trying to say. Could you go a little bit more in-depth?

 

[Count Iblis]

Abbreviation: Sin(x) = S, Cos(x) = C

[S^2 + C^2]/[S (2 C^2 - 1)] =

S/[2 C^2 - 1] (easy to integrate as the derivative of C is -S and S is in the numerator)

+

C^2/[S(2C^2 - 1)]

We can rewrite the numerator of the last term as:

C^2 = 1/2 2 C^2 = 1/2 (2 C^2 - 1 + 1)

This means that you can write the last term as:

1/(2S) + 1/2 * Original term you wanted to integrate.

Then you're done if you can integrate 1/S and that you can do using more or less the same trick:

1/Sin(x) = 1/(2Sin(1/2 x) Cos(1/2 x)) and then replace the numerator by Cos^2(1/2 x) + Sin^2(1/2 x) and you're done.

 

[reaper616]

It works. Very nice. Thank you very much.