MasteringPhysics 8.82: Conservation of Energy/Momentum Problem

[s34n6962]

A 0.150-kg

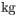frame, when suspended from a coil spring, stretches the spring 0.070 m

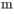. A 0.200-kg

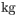lump of putty is dropped from rest onto the frame from a height of 30.0 cm

Find the maximum distance the frame moves downward from its initial position.

To start off the question, I found the Spring Constant of the spring using the fact that if the spring were at equilibrium .070 m away from its relaxed point, the forces of gravity (F=mg) and the force of the spring (F=-kx), should sum up to 0. Therefore mg=kx; so (.15 kg)(9.8 m/s^2)=k(.07 m) so k=21.

Then I found the energy held between the putty and the Earth in potential energy U=mgy; U=(.2 kg)(9.8 m/s^2)(.3 m); and used that to find what it's velocity would be just before it strikes the frame so U=K; (.2 kg)(9.8 m/s^2)(.3 m)=(1/2)(.2 kg)(v)^2; v=((2)(.2)(9.8))^1/2 or roughly 2.42 m/s.

From there I used momentum conservation since the interaction between the putty and frame have outside frictional forces that do work, destroying energy conservation, but retains momentum conservation since the forces are balanced. So mv=mv; (.2 kg)(2.42 m/s)=(.35 kg)v; roughly v=1.39 m/s

Now that I know how fast the interaction between the objects will cause the objects to go I can reapply energy conservation since there are no longer any outside forces that do work on our system, which consists of the frame, the spring, the putty, and earth. So we should obtain the equation (1/2)(.35 kg)(1.39 m/s)+(1/2)(21)(.07 m)^2=(1/2)(21)(x-.07 m)^2-(.35 kg)(9.8 m/s^2)(x), the first term being the kinetic energy of the moving frame/putty, the second being the energy initially stored in the spring, the third being the energy gained by the spring by the interaction, and the fourth being the potential energy lost with gravity since it is moving down. This equation can ultimately be simplified as 10.5x^2-1.96x-.38255=0, which yields a value of x=3.058055537 m, which MasteringPhysics says is very close but that I have a rounding issue, it would be much appreciated if someone would help me mend this miniscule error as it does not allow for partial credit to be given, and it should be noted that I didn't use the rough values to calculate this but rather put in as many as my calculator would give me so I don't believe that that's where my error comes from.

 

[rude man]

You're off by a factor of 10.

Using conservation of energy (potential + spring) solely I came up with 0.348m below the original frame position.[/QUOTE]

 

[haruspex]

the second being the energy initially stored in the spring, the third being the energy gained by the spring by the interaction

Think again about those two terms. Are they the right combination to be using?

 

[s34n6962]

I'm not quite sure what you mean by that, I think they are right, on one side of the Energy Conservation equation I have the Kinetic Energy of the system plus the initial Potential Energy in the Spring equal to the energy gained by the spring after its done moving minus the gravitational potential energy that it loses as it moves down.

 

[rude man]

(p.e. of frame)₁ + (p.e. of putty)₁ + (spring energy)₁ = (p.e. of frame)₂ + (p.e. of putty)₂ + (p.e of spring)₂
since there is no k.e ₁ nor k.e.₂.
That's all you need to solve.
I would pick the zero reference for the p.e. as the level where the spring is relaxed, to simplify the math.

 

[haruspex]

on one side of the Energy Conservation equation I have the Kinetic Energy of the system plus the initial Potential Energy in the Spring equal to the energy gained by the spring after its done moving minus the gravitational potential energy that it loses as it moves down.

Let two energy levels be E₁, E₂. The gain in energy is therefore E₂-E₁. You are saying you have an equation in which the LHS has a term E₁, while the RHS has a term E₂-E₁. Does that seem right?
Anyway, if x₁ and x₂ are two different extensions of the same spring, then the change in energy in going from x₁ to x₂ is not k(x₂-x₁)²/2.

 

[s34n6962]

@rude man, Energy is not conserved throughout the problem, this is because when the putty hits the frame, it is an inelastic collision and has work done upon it by frictional forces, utterly destroying energy conservation within our system since energy is lost due to friction. However during that split-second interaction when the putty and frame collide (before the frame begins to move) momentum is conserved even though energy is not so you have to do an energy conservation, momentum conservation, and then an energy conservation to reach an answer.

@haruspex, There is no gain in energy, as I defined Earth as a part of my system, but are you trying to get at the notion that I should drop my loss of gravitational potential energy? And yes that is the equation for elastic potential energy. Hooke's Law is F=-k(x-x relaxed (where the force of the spring is equal to 0)), now work is force dot distance, or W=(integral) F dot dr, since work equals negative energy we can use Hooke's Law as our force, so U=(integral) k(x-x rel) dx; therefore U=(1/2)(k)(x-x rel)^2. You may not be used to the x rel since it is usually set at x=0 so under most circumstances be ignored, however I set it at x=-.07 so it is actually needed in my equation.

 

[rude man]

@rude man, Energy is not conserved throughout the problem, this is because when the putty hits the frame, it is an inelastic collision and has work done upon it by frictional forces, utterly destroying energy conservation within our system since energy is lost due to friction. However during that split-second interaction when the putty and frame collide (before the frame begins to move) momentum is conserved even though energy is not so you have to do an energy conservation, momentum conservation, and then an energy conservation to reach an answer.

.

Good point. I agree.

 

[s34n6962]

Alright I found my mistake, I slightly miscalculated my c term (It was about midnight when I did it) I had -.38255 whereas I should have had -.336 which threw my answer off enough to give me something close enough for the system to recognize but not to give me the correct answer. So the real equation should be 10.5x^2-1.96x-.336=0 which will end up giving me an answer of x=.2951032793 m which the system accepts as .295 m.

 

[haruspex]

There is no gain in energy, as I defined Earth as a part of my system, but are you trying to get at the notion that I should drop my loss of gravitational potential energy?

No, although I expressed it in generic terms, my point was in respect of your treatment of spring potential energy.
You wrote that
$\frac 12 k {x_0}^2$ is the energy initially stored in the spring (true), and
$\frac 12 k (x-x_0)^2$ is the energy gained by the spring by the interaction.
Surely that's not what you want in the equation. If you have the initial energy on one side then you want the final energy on the other. Subtracting one from the other will give the energy gained by the spring: $\frac 12 k ({x_1}^2-{x_0}^2)$.
Now, as I understand it, your x is the increase in extension, x₁-x₀.
If we forget your description and deduce the gain from your equation we get $\frac 12 k (x_1-2x_0)^2 - \frac 12 k {x_0}^2$, which doesn't look right at all. Maybe you meant to post (1/2)(21)(x+.07 m)^2, not (1/2)(21)(x-.07 m)^2? (I considered that you might be measuring x upwards, but that doesn't fit with what you did with change in gravitational PE.)

 

[s34n6962]

Yes I did, sorry again it was late, it would be minus -.07 which would make it addition.

 

[haruspex]

Yes I did, sorry again it was late, it would be minus -.07 which would make it addition.

OK, glad you got the answer anyway.

 

[s34n6962]

yeah thanks for pointing out the mistake, I actually had that part right on my paper I just typed it up wrong there, the only issue on paper was my calculation of my constant.