pairofstrings
- 411
- 7
- TL;DR Summary
- I have a curve that goes backwards.
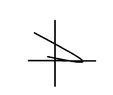
Hello.
I have a curve, I want to write mathematical statements that describes all the features of the curve. For example: how do I write math statement that describes its curvature...
Is it possible to write equation for curves that goes backwards?
Thanks.
I have a curve, I want to write mathematical statements that describes all the features of the curve. For example: how do I write math statement that describes its curvature...
Is it possible to write equation for curves that goes backwards?
Thanks.