Math Help for Advanced Simulation of Twin Paradox

[Jeronimus]

In my infamous simulation of the twin paradox, i assume a near instantaneous acceleration, with the results being almost identical with the "real" thing sub some extremely small values which you could not see with the naked eye anyway.

But i might want to take the simulation a step further, to give the exact value for slower accelerations.

For the near instantaneous case, as an example.

When two observers A and B are e local to each other, and B accelerates to 0.6c near instantaneously, then an event which B measured to be at x=1ls, t=0s pre-acceleration, post acceleration he will measure to be almost exactly at.

x' = γ(x-vt) = 1.25ls
t' = γ(t-vx/c²) = - 0.75s

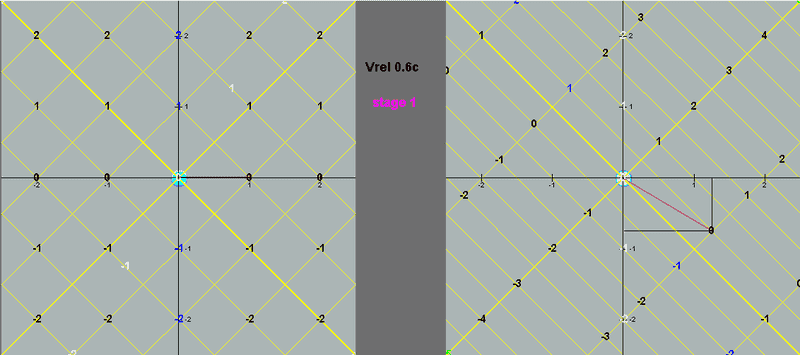
Increasing the acceleration, we would get arbitrary close to those two values.

Now i could of course do the acceleration in small steps, accelerating to a given v, then let some time pass. The more steps, the closer i would get to the real value. But that would be too intensive computational and would not really be "perfect". Again i would have to work with just an approximation.

Is there any way to get the exact values for x' and t' for let's say the case of the accelerating observer B measuring the acceleration towards 0.6c to be taking 1 second on his clock?

Is it calculable without having to do it in "steps" where you could get arbitrary close to the results, but never get the exact results?

 

[PeroK]

The worldline of a simply accelerating observer is given by:

$t = \frac{c}{a} sinh(\frac{a\tau}{c}), \ x = \frac{c^2}{a}(\cosh(\frac{a\tau}{c}) - 1)$

Where $a$ is the acceleration and $\tau$ is the proper time of the observer.

 

[Jeronimus]

The worldline of a simply accelerating observer is given by:

$t = \frac{c}{a} sinh(\frac{a\tau}{c}), \ x = \frac{c^2}{a}(\cosh(\frac{a\tau}{c}) - 1)$

Where $a$ is the acceleration and $\tau$ is the proper time of the observer.

Can you give an example where you compute x' and t' for the case i described above, where observer B accelerates to 0.6c within 1 seconds from his perspective, hence when he reaches 0.6c, his clock would display 1 second. At 0.5sec on his clock he would be at 0.3c etc.

Where would the event x=1ls t=0s be located when measured by B post acceleration, using the acceleration profile described above?

 

[PeroK]

Can you give an example where you compute x' and t' for the case i described above, where observer B accelerates to 0.6c within 1 seconds from his perspective, hence when he reaches 0.6c, his clock would display 1 second. At 0.5sec on his clock he would be at 0.3c etc.

Where would the event x=1ls t=0s be located when measured by B post acceleration, using the acceleration profile described above?

I assumed you wanted to do the calculation. I can't say I'm entirely sure why you want to do it, but I thought the worldline might help.

 

[Jeronimus]

I assumed you wanted to do the calculation. I can't say I'm entirely sure why you want to do it, but I thought the worldline might help.

I might want to improve the simulation at some later time such that it gives exact results and can deal with non-instantaneous accelerations.

 

[PeroK]

I might want to improve the simulation at some later time such that it gives exact results and can deal with non-instantaneous accelerations.

Do you know what a worldline is? Do you understand the one I posted?

 

[Jeronimus]

Do you know what a worldline is? Do you understand the one I posted?

I sure do know what a worldline is (which you should have figured out by now, going by my past posting history). The one you posted i do understand, except the "proper time" part. Proper time escapes me...

edit: "In relativity, proper time along a timelike world line is defined as the time as measured by a clock following that line." - from wikipedia

That sounds simple enough i guess. I would appreciate an example calculation still, just to make sure i got it right.

 

[PeroK]

I sure do know what a worldline is (which you should have figured out by now, going by my past posting history). The one you posted i do understand, except the "proper time" part. Proper time escapes me...

The proper time of an observer is the time shown on her clock.

Although it's just my opinion, studying the worldline I posted may be more useful in terms of understanding SR than what you are doing, the answer to which I suspect is fairly meaningless. But, don't let that stop you if you like your problem. It's certainly not an easy one.

 

[Jeronimus]

The proper time of an observer is the time shown on her clock.

Although it's just my opinion, studying the worldline I posted may be more useful in terms of understanding SR than what you are doing, the answer to which I suspect is fairly meaningless. But, don't let that stop you if you like your problem. It's certainly not an easy one.

Your opinion has been noted. Personally however, it is my opinion that you can learn a lot by trying to create an accurate relativistic simulation. Especially if i ever get to the point where it will include the ability to show the probability of detecting particles within a certain volume of space/spacetime?... a bit ambitious given my current state but who knows... maybe in the next life.

 

[PAllen]

Can you give an example where you compute x' and t' for the case i described above, where observer B accelerates to 0.6c within 1 seconds from his perspective, hence when he reaches 0.6c, his clock would display 1 second. At 0.5sec on his clock he would be at 0.3c etc.

Where would the event x=1ls t=0s be located when measured by B post acceleration, using the acceleration profile described above?

Solve for acceleration such that dx/dt is .6 when tau is 1. That should be a straightforward, if cumbersome, computation. Since that is enough to determine the accelaeration, you don't get to pick anything else unless you want to go beyond uniform acceleration for the nonertial sections of world lines.

 

[Jeronimus]

$t = \frac{c}{a}$ doesn't that give me 1/s in units?

$sinh(\frac{a\tau}{c})$ while this becomes unitless

shouldn't i be getting s(seconds) as units when solving for t using this formula $t = \frac{c}{a} sinh(\frac{a\tau}{c})$ ?

 

[Jeronimus]

^ never mind the above, my mind was playing tricks on me again.

I think i understand the formulas now and know how to implement it.