Math Myth: Parallels do not intersect

[Greg Bernhardt]

From @fresh_42's Insight
https://www.physicsforums.com/insights/10-math-things-we-all-learnt-wrong-at-school/

Please discuss!

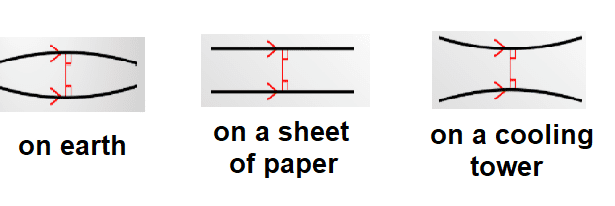
Have you ever stood on a railroad track? Nobody would deny that the rails are in parallel. Do they intersect? Certainly not soon because locomotives normally do not derail. However, you will likely have looked to the horizon while standing on the rails. And - surprise - they do intersect at the horizon, or mathematically: at infinity. But infinity on a ball where we live isn't at infinity. It is actually somewhere. We see that there are possible geometries, in which parallels do intersect.

 

[.Scott]

High School Geometry is 99% Euclidean. And in that context, parallel lines do not intersect. If you are taking about railroad tracks on a spherical surface, technically they are not lines, but arcs following the spherical surface. If you make railroad tracks great circles, the will intersect about 6000 miles from their usable zone.

 

[Stephen Tashi]

Less controversial is that we should not define parallel lines to be a pair of lines that do not intersect - since this is the case in 3D Euclidean Geometry, which is a familiar topic. So what is the best definition for "parallel lines" from the viewpoint of making a definition that works well in all types of geometries?

 

[martinbn]

Less controversial is that we should not define parallel lines to be a pair of lines that do not intersect - since this is the case in 3D Euclidean Geometry, which is a familiar topic. So what is the best definition for "parallel lines" from the viewpoint of making a definition that works well in all types of geometries?

It would depend on what you need the definition for.