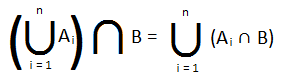Mathematical Induction question

[William1]

A question I'm working on and my math book doesn't clarify the answer well enough for me to follow. I'm having some issues at getting the math symbols to work correctly so bare with me!Prove by mathematical induction that if A₁, A₂, ..., A_n and B are any n + 1 sets, then:
View attachment 37
Base step = n = 1 so P(1): A₁ ∩ B = A₁ ∩ B
Induction Step: LHS of P(k+1):

Substitute (k+1) for all N. Working LHS: (where {k U i = 1}A_i is the union from 1 to n of A_k)
=(({k U i = 1}A_i​) U A_k+1) ∩ B; then distribute:
=(({k U i = 1}(A_i​ ∩ B) U ( A_k+1 ∩ B)

then this is where I get stuck. I feel there is about one or two more steps but I can't seem to grasp it. Any suggestions?

 

[Plato2]

Prove by mathematical induction that if A₁, A₂, ..., A_n and B are any n + 1 sets, then:
https://www.physicsforums.com/attachments/37

$\bigcup\limits_{k = 1}^{N + 1} {\left( {A_k \cap B} \right)} = \bigcup\limits_{k = 1}^N {\left( {A_k \cap B} \right)} \cup \left( {A_{N + 1} \cap B} \right)$
$ = \left[ {\left( {\bigcup\limits_{k = 1}^{N } { {A_k }} } \right) \cap B} \right] \cup \left( {A_{N+1 } \cap B} \right)$
$ = \left[ {\left( {\bigcup\limits_{k = 1}^{N } { {A_k } } } \right) \cup A_{N+1 } } \right] \cap B$.

Can you finish?

 

[William1]

Wouldn't it just be:

= {k+1 U i = 1 A_i U A_k+1) ∩ B
= {k+1 U i = 1} (A_i ∩ B)

 

[Plato2]

Wouldn't it just be:
= {k+1 U i = 1 A_i U A_k+1) ∩ B
= {k+1 U i = 1} (A_i ∩ B)

Do you see that $\left( {\bigcup\limits_{k = 1}^N {A_k } } \right) \cup A_{N + 1} = \bigcup\limits_{k = 1}^{N + 1} {A_k } ~?$

I started with $P(N)$ being true.
Then looked at the expansion of $P(N+1)$.

 

[William1]

Yes, I sort of see how they are equal. It's still not crystal clear to me yet though.

 

[Plato2]

Yes, I sort of see how they are equal. It's still not crystal clear to me yet though.

Can you see that $\sum\limits_{k = 1}^{n + 1} {a_k } = a_1 + a_2 + \cdots + a_{n + 1} = \left( {a_1 + a_2 + \cdots + a_n } \right) + a_{n + 1} ~?$

If so $\sum\limits_{k = 1}^{n + 1} {a_k } =\sum\limits_{k = 1}^{n} {a_k }+ a_{n + 1} $

 

[William1]

Yes, I see that.

 

[Plato2]

Yes, I see that.

Then what are you missing in understanding the induction proof?