- #1
cdrake3
- 3
- 0
I have a difficult problem on my research exploration for math. I am modeling the convection currents of boiling water in a pot, which is heated by an electric stove. There is a constant supply of energy at 8000 watts (the average for a stove) that heats the pot from the bottom of the pot, which has a circular base.
My Assignment: I have to create a 2-D mathematical model for a convection current in a cylinder object with heat source on bottom late – then demonstrating a slope field for the velocity of water as it rises. I have to solve for various velocities throughout the position of the pot. For example, I must generate an equation that models this phenomenon and a 2-D Graph (slope field) from it – looking something like this (just an example – the below is not the correct graph for the convection situation that I’m modeling):
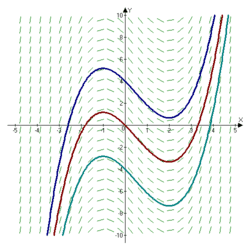Where I’m Stuck: Currently, I’m not quite sure of how I should go approaching this problem; specifically what is the right governing math equation (formula) for this situation:
• 2-D convection current
• Cylindrical shape
• Circular plate heat source underneath (8,000 watts)
In addition, I need to find the right formula that will create a model for a slope field – such that I can product a graph from it (to model convection velocities).
I have some research done below – but I’m not finding the right-fit formula to address my problem. There seems to be several physics and mathematical expressions that come together for the solution I seek – but I don’t know how exactly or if I am following the right approach. Here goes:
General Convection-Diffusion Equation:
The general equation is:
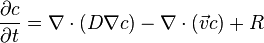
where
• c is the variable of interest (species concentration for mass transfer, temperature for heat transfer),
• D is the diffusivity (also called diffusion coefficient), such as mass diffusivity for particle motion or thermal diffusivity for heat transport,
• v is the average velocity that the quantity is moving. For example, in advection, c might be the concentration of salt in a river, and then would be the velocity of the water flow. As another example, c might be the concentration of small bubbles in a calm lake, and then would be the average velocity of bubbles rising towards the surface by buoyancy (see below).
• R describes "sources" or "sinks" of the quantity c. For example, for a chemical species, R>0 means that a chemical reaction is creating more of the species, and R<0 means that a chemical reaction is destroying the species. For heat transport, R>0 might occur if thermal energy is being generated by friction.
• ∇ represents gradient and represents divergence.
There is more information that I am using in the link below:
http://en.wikipedia.org/wiki/Convection–diffusion_equation#General
Where do I go from here?: from this point, I’m totally lost on if the above general equation is correct or not for my specific problem – and if it is, then how do I apply it?
Beyond that, I need to create a mathematical model for the slope field of convection current velocities – which is my ultimate aim for the overall assignment.
Can you help me to organize my approach from here?
How do I apply the general formula above? Considering that I have a 2-D cylinder problem and a 1-side heat source (bottom circle surface).
Do you have any guidance on slope field formulas/equations?
I thank you for your help in advance – I am hoping that you can help point me in the right direction.
My Assignment: I have to create a 2-D mathematical model for a convection current in a cylinder object with heat source on bottom late – then demonstrating a slope field for the velocity of water as it rises. I have to solve for various velocities throughout the position of the pot. For example, I must generate an equation that models this phenomenon and a 2-D Graph (slope field) from it – looking something like this (just an example – the below is not the correct graph for the convection situation that I’m modeling):
• 2-D convection current
• Cylindrical shape
• Circular plate heat source underneath (8,000 watts)
In addition, I need to find the right formula that will create a model for a slope field – such that I can product a graph from it (to model convection velocities).
I have some research done below – but I’m not finding the right-fit formula to address my problem. There seems to be several physics and mathematical expressions that come together for the solution I seek – but I don’t know how exactly or if I am following the right approach. Here goes:
General Convection-Diffusion Equation:
The general equation is:
where
• c is the variable of interest (species concentration for mass transfer, temperature for heat transfer),
• D is the diffusivity (also called diffusion coefficient), such as mass diffusivity for particle motion or thermal diffusivity for heat transport,
• v is the average velocity that the quantity is moving. For example, in advection, c might be the concentration of salt in a river, and then would be the velocity of the water flow. As another example, c might be the concentration of small bubbles in a calm lake, and then would be the average velocity of bubbles rising towards the surface by buoyancy (see below).
• R describes "sources" or "sinks" of the quantity c. For example, for a chemical species, R>0 means that a chemical reaction is creating more of the species, and R<0 means that a chemical reaction is destroying the species. For heat transport, R>0 might occur if thermal energy is being generated by friction.
• ∇ represents gradient and represents divergence.
There is more information that I am using in the link below:
http://en.wikipedia.org/wiki/Convection–diffusion_equation#General
Where do I go from here?: from this point, I’m totally lost on if the above general equation is correct or not for my specific problem – and if it is, then how do I apply it?
Beyond that, I need to create a mathematical model for the slope field of convection current velocities – which is my ultimate aim for the overall assignment.
Can you help me to organize my approach from here?
How do I apply the general formula above? Considering that I have a 2-D cylinder problem and a 1-side heat source (bottom circle surface).
Do you have any guidance on slope field formulas/equations?
I thank you for your help in advance – I am hoping that you can help point me in the right direction.