Mathematical modeling of driveline impact test of an automobile

[k.udhay]

TL;DR

How to consider the effect of spring in a mathematical model of a car with specific GVW?

I am in a process of making a mathematical model of an automobile driveline validation procedure called "Driveline impact". In this test, after the engine in cranked, first gear is selected. While clutch pedal is still pressed, engine rpm is raised unto its max. torque deliverable speed. In this condition, the clutch is snap released allowing an impact torque to pass through the driveline. In spite of the max. torque governing system, I understand a momentary higher torque will be transferred, as all such governing systems are responsive in nature.

For the purpose of simplicity, I am thinking of considering only the three elements that majorly contribute:
1. The engine or motor that can produce any torque (ignoring effect of torque governing)
2. Clutch - To consider the effect of its stiffness
3. Vehicle with a GVW

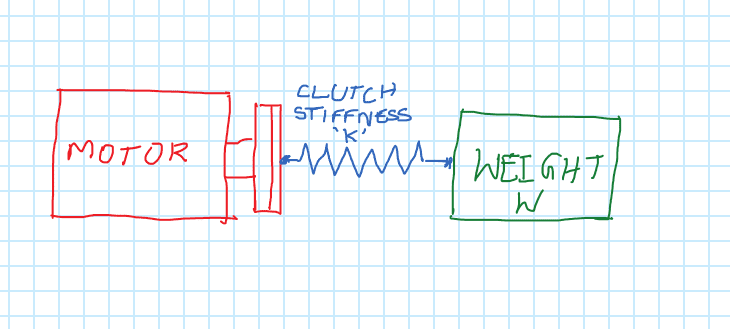
Objective:
To plot the time vs. torque curve and therefore finding the max. torque point

Help required:
I have no clue as how to start. Especially I am unable to figure out to find the torque demand from vehicle. If someone can help me with a suitable derivation lecture available in the internet, that would mean a lot to me.

 

[Baluncore]

Can you assume that the wheels do not spin?

Rotational energy stored in the motor and flywheel will flow to the clutch where it provides a torque to the gearbox input shaft and frictional heat as the clutch initially must slip.

You need to model the flow of stored energy from the motor to the vehicle kinetic energy via the slipping clutch.

Power is the rate of flow of energy. Power is also torque times RPM. If the drive shaft is at zero RPM, no work is being done because at zero RPM, the torque for any power would be infinite. Once the shaft starts to rotate energy transfer begins as the vehicle starts to move.

The torque in the driveline is limited by clutch slip.

 

[k.udhay]

Thanks Baluncore. I can't assume gearbox input shaft speed as zero as you correctly mentioned that it will mean the torque to be infinite. My very purpose of doing this activity is to find the closest accurate torque at gearbox input shaft.

 

[JBA]

Edit:
The maximum instant input shaft torque will be at the front of the driveshaft and controlled by a combination of the clutch load limit, the rotational inertia of the gearbox components, the driveshaft and all of the rear drive assembly components, including wheels and tires; plus, the rear tire's breakaway friction coefficient times vehicle's percent of weight on those rear tires.

 

[Baluncore]

The engine and gearbox mounts, along with the vehicle suspension are all elastic and form a loop including the drive-line and the differential housing. That drive-loop stores energy proportional to it's deflection. The gearbox is inside that drive loop.

As the clutch is released, and as the vehicle starts to move, rotational energy from the motor and flywheel “winds up” and stores energy in that elastic drive loop. During that period the torque increases to a maximum. As the vehicle accelerates due to increasing wheel torque, the RPM of the wheels increase, which reduces the drive loop torque until wheel speed matches the engine speed. Torque is then due to continuous engine power = rate of energy conversion.

Simulation will involve the conservation of energy, simple accounting.
To model the system you will need state variables for;
Engine RPM, which can give you stored rotational energy.
Vehicle speed, which can give you stored kinetic energy.
Drive loop torque, elastic deflection which gives you stored potential energy.
(edit) Clutch temperature, which gives you lost energy due to clutch slip.

Consider an analog; A moving mass (representing the spinning engine) is about to pass a stationary mass (the vehicle). As they pass, a zero length spring (the drive loop) is connected between the two masses. As spring tension increases, the stationary mass is accelerated while the moving mass is decelerated until they have the same velocity. The maximum tension in the spring represents maximum torque in the drive loop during clutch release.

Above a certain torque, the clutch will slip, that will waste energy as heat, which will be lost from the system. I have ignored damping of the system that would, in the absence of losses cause oscillation. Oscillation of the real system could cause clutch shudder, or make the vehicle accelerate in a series of jumps; AKA kangaroo clutch.

 

[k.udhay]

The engine and gearbox mounts, along with the vehicle suspension are all elastic and form a loop including the drive-line and the differential housing. That drive-loop stores energy proportional to it's deflection. The gearbox is inside that drive loop.

As the clutch is released, and as the vehicle starts to move, rotational energy from the motor and flywheel “winds up” and stores energy in that elastic drive loop. During that period the torque increases to a maximum. As the vehicle accelerates due to increasing wheel torque, the RPM of the wheels increase, which reduces the drive loop torque until wheel speed matches the engine speed. Torque is then due to continuous engine power = rate of energy conversion.

Simulation will involve the conservation of energy, simple accounting.
To model the system you will need state variables for;
Engine RPM, which can give you stored rotational energy.
Vehicle speed, which can give you stored kinetic energy.
Drive loop torque, elastic deflection which gives you stored potential energy.
(edit) Clutch temperature, which gives you lost energy due to clutch slip.

Consider an analog; A moving mass (representing the spinning engine) is about to pass a stationary mass (the vehicle). As they pass, a zero length spring (the drive loop) is connected between the two masses. As spring tension increases, the stationary mass is accelerated while the moving mass is decelerated until they have the same velocity. The maximum tension in the spring represents maximum torque in the drive loop during clutch release.

Above a certain torque, the clutch will slip, that will waste energy as heat, which will be lost from the system. I have ignored damping of the system that would, in the absence of losses cause oscillation. Oscillation of the real system could cause clutch shudder, or make the vehicle accelerate in a series of jumps; AKA kangaroo clutch.

I have started thinking in the exact same way. You can look at my post in another forum:

https://tinyurl.com/y68lp292

Now the challenging part is to find how fast is the stored potential energy drained through clutch. If someone can give me the direction to solve the questions asked in the link above, I think I will be able to make it.

 

[Baluncore]

You will need to specify some parameters;
1. Initial engine RPM, at the instant the clutch is released.
2. Inertia of the engine, so you can compute the rotational energy stored in the motor.
3. Stiffness of the elastic drive loop. (torque / radian).
4. Mass of the vehicle.
Then write out the equations and model the system.

 

[JBA]

All of the above apply for a rigorous solution; but, the most basic analysis of maximum input shaft torque vs the vehicle weight, assuming all other internal factors listed equal, will be either the torque at the breakaway point the rear tires or the inertial resistance of the vehicle at launch whichever is less; and, since both are determined by the vehicle weight, the one of those two found responsible for anyone vehicle weight will apply for all vehicle weights. It is the resistance to the engine torque that controls rather than the engine torque provided.