- #1
pairofstrings
- 411
- 7
Hi.
I am trying to understand the images that I have posted below.


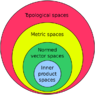
Each layer of Mathematical Structure Hierarchy in the image in this post and Mathematical Space Hierarchy in the image in this post are: statements.
1. What do these statements of each layer of these hierarchies in the images in this post let's me do?
2. Do these statements let's me build something?
3. What if there is no Mathematical Structure Hierarchy and Mathematical Space Hierarchy?
4. Why did somebody create Mathematical Structure Hierarchy and Mathematical Space Hierarchy?
5. Do these Mathematical Structure and Mathematical Space Hierarchies exist to describe something?
6. Why each layer of Mathematical Structure Hierarchy and Mathematical Space Hierarchy be in the order as they are shown in the images above? Can they be jumbled?
I have asked these questions to know what Mathematical Space Hierarchy is and what Mathematical Structure Hierarchy is.
- Trying to connect dots.
Thanks!
I am trying to understand the images that I have posted below.
Each layer of Mathematical Structure Hierarchy in the image in this post and Mathematical Space Hierarchy in the image in this post are: statements.
1. What do these statements of each layer of these hierarchies in the images in this post let's me do?
2. Do these statements let's me build something?
3. What if there is no Mathematical Structure Hierarchy and Mathematical Space Hierarchy?
4. Why did somebody create Mathematical Structure Hierarchy and Mathematical Space Hierarchy?
5. Do these Mathematical Structure and Mathematical Space Hierarchies exist to describe something?
6. Why each layer of Mathematical Structure Hierarchy and Mathematical Space Hierarchy be in the order as they are shown in the images above? Can they be jumbled?
I have asked these questions to know what Mathematical Space Hierarchy is and what Mathematical Structure Hierarchy is.
- Trying to connect dots.
Thanks!