Mathematically expressing field driven water autoionization

[HelloCthulhu]

I recently read a paper on using an electric field to drive water autoionizaton. I'm trying to figure out how to use the Laplace equation on pg 9; 4th paragraph; to solve for voltage. I'm also interested in how this equation would change if I replaced the hemispherical tip with a parallel plate. Anyone strongly familiar with this subject matter? Any help is greatly appreciated!

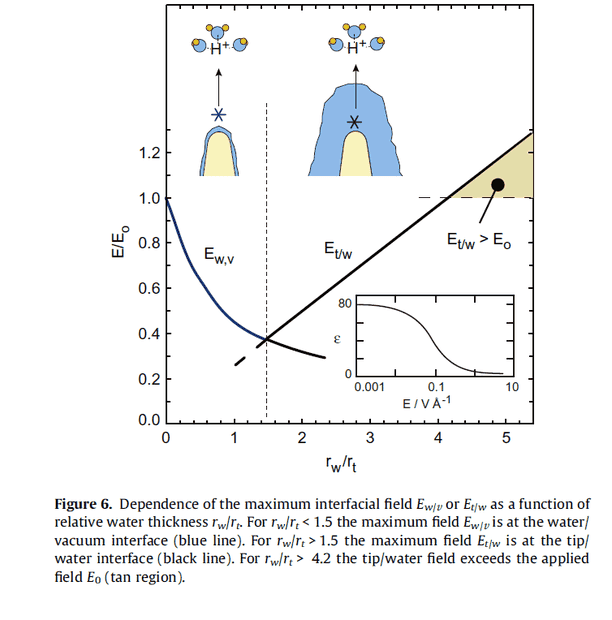
https://www.sciencedirect.com/science/article/abs/pii/S0009261411011511

 

[TeethWhitener]

I haven’t run through the math specifically, but it’ll be the Poisson equation no matter what, but the boundary conditions will change. So for parallel plates, you’ll want to look at the Laplacian in Cartesian coordinates instead of spherical coordinates as your starting point.

 

[HelloCthulhu]

Thank you for the response! I still have some questions about the variables. I know how to use Figure 6 to find the values for maximum interfacial field E_w/v or E_t/w and water thickness r_w/r_t, but I'm still not sure what to do with ∈(E), d, or how to solve for ϕ_w or ϕ_v.

In the end, all I'm really trying to figure out is what the electric the field between the molecules and the electrode has to be in order to cause water to ionize. Some of the fundamentals seem comparative to Paschen's Law (Electric Field = voltage x distance). As for adjusting that equation for parallel plates I think I've found an explanation on what it should look like, but I'm still far too ignorant about electrostatics for it to make any real sense to me yet. Thank you for your input so far, I hope you can continue to help me with this.

http://jsa.ece.illinois.edu/ece329/notes/329lect07.pdf

 

[TeethWhitener]

It’s unclear how much background knowledge you have and if this problem is at the right level for you. For instance, I don’t see a $d$ being used as a variable in any of these images. The only $d$’s I see denote derivatives.

To get the potential (aka the voltage), you would solve the Poisson/Laplace equation for $\phi$, given the appropriate boundary conditions. I doubt there’s an analytical way to do it without a really simple functional form for $\epsilon(E)$, but it should be possible to write a code to get a numerical solution. To get the electric field, you take the gradient of the potential (assuming the system is time-invariant).

 

[HelloCthulhu]

It’s unclear how much background knowledge you have and if this problem is at the right level for you. For instance, I don’t see a d being used as a variable in any of these images. The only d’s I see denote derivatives.

It's far beyond anything I have experience with. I've solved derivatives in the past, but wasn't familiar with second derivatives. To be honest, I'm in way over my head on these subjects. But even so I'd like to keep working on trying to understand them. Thank you so much for your help.

 

[TeethWhitener]

It's far beyond anything I have experience with. I've solved derivatives in the past, but wasn't familiar with second derivatives. To be honest, I'm in way over my head on these subjects. But even so I'd like to keep working on trying to understand them. Thank you so much for your help.

I would advise you to learn single and multivariable calculus as well as vectors before trying to tackle E&M.