Mathematics modeling for a Mass-Spring-Damper system

[Devs]

Homework Statement

It has no statement

Relevant Equations

mx''+bx'+kx=p(t)

Summary:: How can I get mathematics modeling for these tree systems?

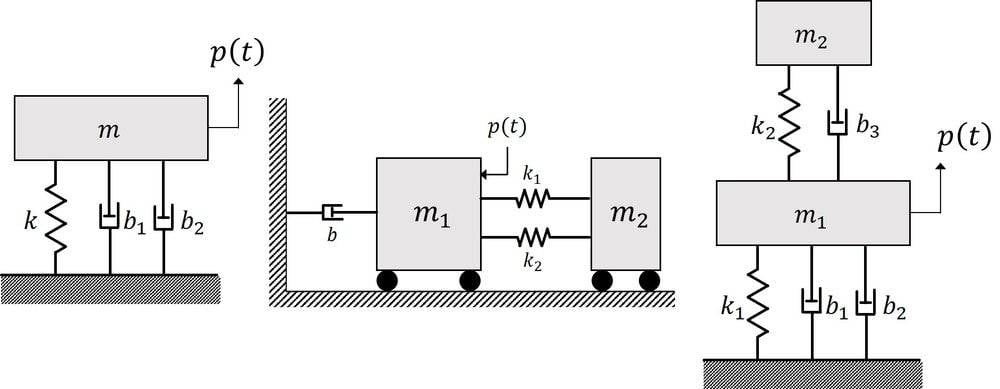
First of all, my mother tongue is not English, so my expression could be ambiguous.

I want to get mathematics modeling for these three system above, like this form.

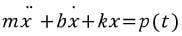
First one is b -> (b1+b2), right? but I'm not sure about second and third figures.
After that, do I have to do Laplace Transform?

+Can I get Damping ratio and Natural frequency for all these systems? These are not necessary. Only mathematics modelings are also thank you.
I wanted to ask questions on Korean sites before, but I couldn't find appropriate site. Please help me.
Thank you all for your help.[Moderator's note: Moved from a technical forum and thus no template.]

 

[Devs]

what means 'thus no template'?

 

[fresh_42]

what means 'thus no template'?

It is a relict when we had a template in the homework forum but not elsewhere. I have yet to adjust it.
It is primarily a note for other mentors not to move it again, and that it is approved as homework in the sense that it shows some efforts from your side which we require in the homework sections.

 

[Chestermiller]

Are you asking how to formulate the equations for these various 1- and 2 degrees of freedom problems, or are you asking how to solve the equations once you have the equations?

 

[Devs]

Are you asking how to formulate the equations for these various 1- and 2 degrees of freedom problems, or are you asking how to solve the equations once you have the equations?

There is no given equation. I'm asking how to formulate the equation. Thank you for asking me easily.

 

[Chestermiller]

Are you familiar with Newton's 2nd law of motion?

 

[Devs]

Are you familiar with Newton's 2nd law of motion?

I know that formula is 'F=m*dv/dt=ma'

 

[Chestermiller]

OK. Let's take as an example the middle figure. We are going to be solving for the motion of the two masses, as characterized by $x_1(t)$ and $x_2(t)$ which are the coordinates of the centers of mass of M1 and M2, respectively (as functions of time). Are you OK with this so far?

 

[Devs]

yes I got that

 

[Chestermiller]

The tension is spring k1 is $$k_1(x_2-x_1-L_1)$$ where $L_1$ is the distance between the centers of the two masses when the tension in the spring is zero.

The tension of dashpot b is $$b\left(\frac{dx_1}{dt}-0\right)$$ where the 0 signifies the velocity at the left end of dashpot b. A better example is the tension of dashpot b3 in the third figure: $$b_3\left(\frac{dy_2}{dt}-\frac{dy_1}{dt}\right)$$Based on these relationships, what is the net force acting on mass m1 in example 2, and what is the net force acting on mass m2 in example 2?