Engineering MATLAB Exercise on DFT

[marco02]

Homework Statement

ddòd

Relevant Equations

lsd

Good morning, I have an exercise with two points that gives a Matlab mat file in which are contained the samples of two measured signals and the variable fs indicating the sampling frequency

A)Signal 1 consists of two sinusoidal signals of which you are asked to calculate: -the duration ⇒ I thought is found by doing T=N/fs where N is the number of samples (in my case 512); -the two frequencies (enter in ascending order). I used the following Matlab commands to plot the Fourier transform:

s1=datafile1;
N=512;
f=(-fs/2):(fs/N):(fs/2-fs/N);
S1=fftshift(fft(s))
plot(f,abs(S1))

I got this

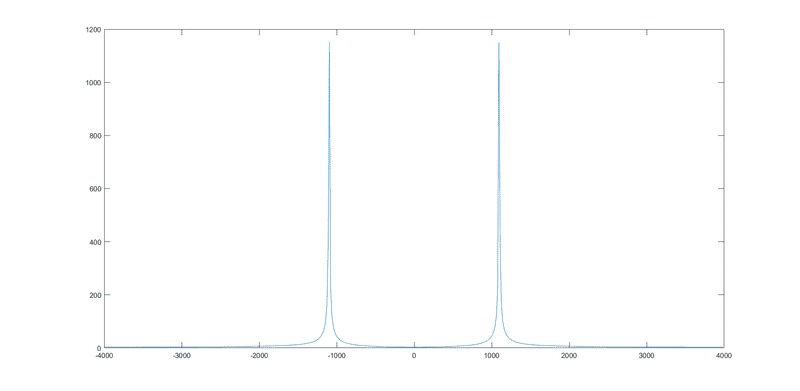
Is it right then to take as frequencies the ones I see in the two peaks(positive and negative with the same modulus)?

B)Signal 2 consists of the superposition of a larger number of sinusoidal signals. You are asked to identify the frequencies present by placing them in the boxes in ascending order(there are 6 boxes). If the number of frequencies identified is less than the number of boxes available, enter the value of the sampling frequency in the unnecessary boxes.

In the second case I get this

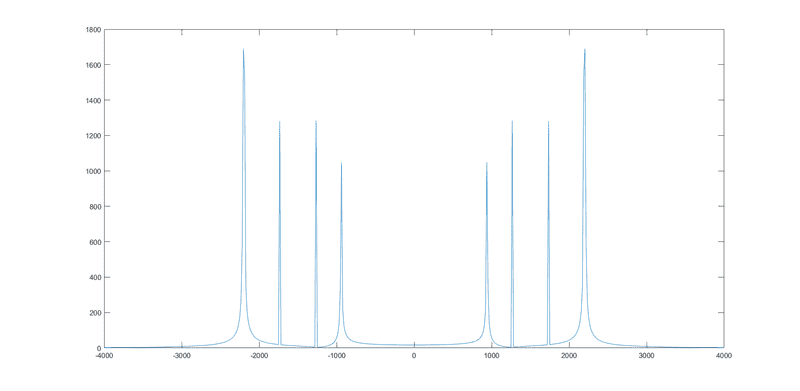
How do I choose the frequencies now if I have 8 peaks?
The mat file is provided below



Thanks to those who will help me

 

[scottdave]

Fourier transform plots always show the frequency and a "mirror image" negative of the same frequency. See the Mathworks help https://www.mathworks.com/help/matlab/math/fourier-transforms.html

So your first plot indicates a single frequency.

I suggest creating some data samples from known frequencies to see if the Fourier plots are what you expect.