tworitdash
- 104
- 25
I have a Gaussian shape frequency domain spectrum of which I am calculating the Inverse Fourier transform. I use both IFFT of MATLAB and also an analytical expression of Mathematica. They are not the same.
I don't know where it is wrong. I have pasted both the figures. The numerical one has been zoomed in actually because the time domain pulse came out to be too thin. Any help is appreciated.The code is below:
[CODE lang="matlab" title="MATLAB code for IFFT with Analytical equation"]clear;
% close all;lambda = 0.03;
PRT = 1e-3;
mu = 4; % Mean Doppler
sigma = 0.2;
v_amb = 7.5;
N = 60000; % Total number of points in time axis
t1 = 0:PRT:(N - 1)*PRT; % Time axis
vel_axis = linspace(-v_amb, v_amb, N); % velocity axis for the entire rotation
% vel_axis_hs = linspace(-v_amb, v_amb, hs); % velocity axis for one beamwidth
% t1 = -N/2*PRT:PRT:(N/2 - 1)*PRT; % Time axis
% s_analyt_o = 1./sqrt(2*pi*(sigma).^2) .* exp(-(vel_axis - mu).^2./(2*(sigma).^2));
% SNR = 10^(30/10);
% X = rand(1, N);
% Theta = 2 .* pi * rand(1, N);S_ = gaussmf(vel_axis, [sigma, mu]);
% Noise = sum(S_) ./ (N .* SNR);
% s_analyt_o = -(S_ + Noise) .* log(X);
s_analyt_o = S_;
s_num = ifft(ifftshift(sqrt(s_analyt_o))); % Numerical IFFTs_analyt = ifftshift((2/pi)^(1/4) * sqrt(sigma) .* exp(-t1 .* ((sigma)^2 .* t1 + 1j .* mu))); % analytical IFFT
figure; plot(t1, abs((s_analyt)));
figure; plot(t1, abs(ifftshift(s_num)));[/CODE]
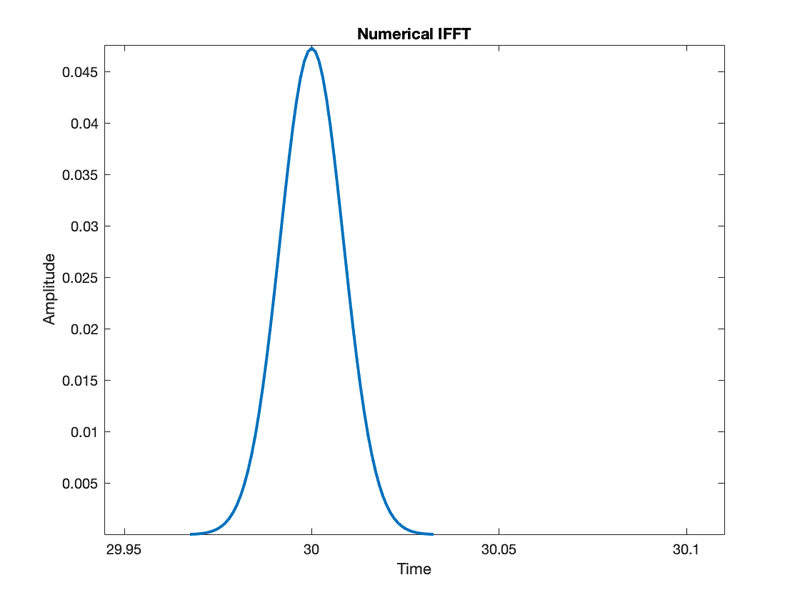
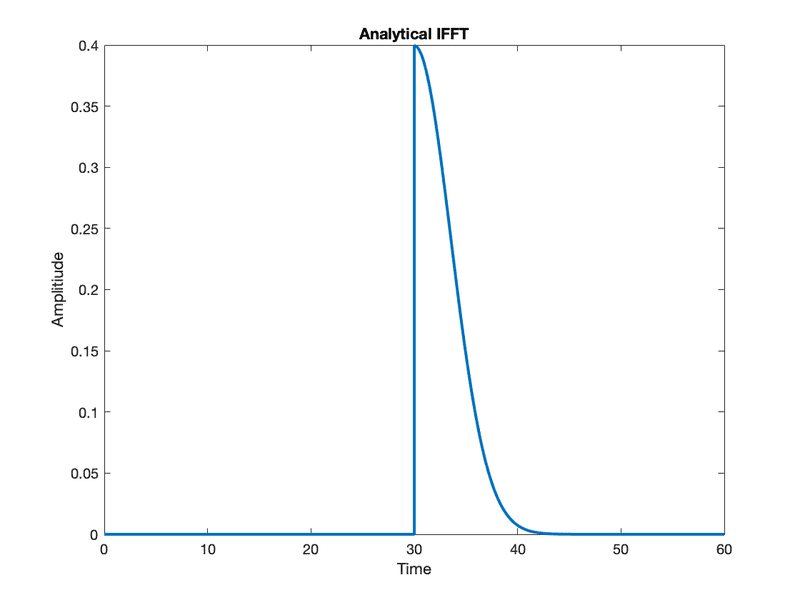
I don't know where it is wrong. I have pasted both the figures. The numerical one has been zoomed in actually because the time domain pulse came out to be too thin. Any help is appreciated.The code is below:
[CODE lang="matlab" title="MATLAB code for IFFT with Analytical equation"]clear;
% close all;lambda = 0.03;
PRT = 1e-3;
mu = 4; % Mean Doppler
sigma = 0.2;
v_amb = 7.5;
N = 60000; % Total number of points in time axis
t1 = 0:PRT:(N - 1)*PRT; % Time axis
vel_axis = linspace(-v_amb, v_amb, N); % velocity axis for the entire rotation
% vel_axis_hs = linspace(-v_amb, v_amb, hs); % velocity axis for one beamwidth
% t1 = -N/2*PRT:PRT:(N/2 - 1)*PRT; % Time axis
% s_analyt_o = 1./sqrt(2*pi*(sigma).^2) .* exp(-(vel_axis - mu).^2./(2*(sigma).^2));
% SNR = 10^(30/10);
% X = rand(1, N);
% Theta = 2 .* pi * rand(1, N);S_ = gaussmf(vel_axis, [sigma, mu]);
% Noise = sum(S_) ./ (N .* SNR);
% s_analyt_o = -(S_ + Noise) .* log(X);
s_analyt_o = S_;
s_num = ifft(ifftshift(sqrt(s_analyt_o))); % Numerical IFFTs_analyt = ifftshift((2/pi)^(1/4) * sqrt(sigma) .* exp(-t1 .* ((sigma)^2 .* t1 + 1j .* mu))); % analytical IFFT
figure; plot(t1, abs((s_analyt)));
figure; plot(t1, abs(ifftshift(s_num)));[/CODE]
