Matlab ODE Problem (paritcle trajectory)

[intrepid44]

Hi, I currently have this problem to solve, and I'm quite stuck. I would much appreciate it if anyone could point me in the direction on how to solve it.

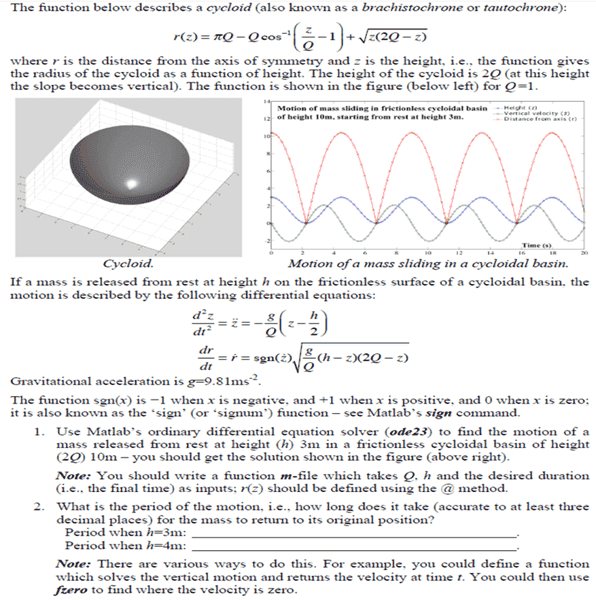
This is my go at it, although currently I don't have access to MATLAB until tomorrow as the university library has now closed.

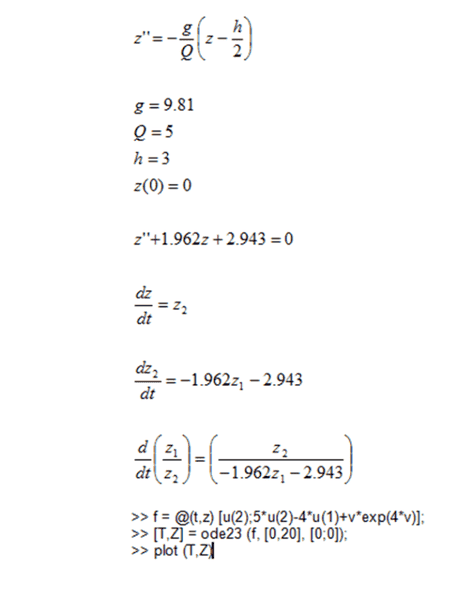
Is this the correct way to get the motion? If I then turn it into a function?

Many thanks.

Regards,
intrepid44

 

[intrepid44]

The last bit should be: >> f = @(t,z) [z(2);-1.962*z(1)-2.943];

 

[intrepid44]

Got it sorted, never mind.