- #1
Nikki16
- 6
- 0
Matrices- Variable in Matrices-Help!
1-19-12
I need help. I have a homework question that I have tried to solve.
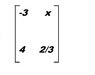
The matrix in the attachment has no inverse. Explain how you can determine the value of x. Then find x.
I tried cross multiplying.
3*2/3=4x
6/3=4x
2=4x
x=2/4
x=1/2
1-19-12
I need help. I have a homework question that I have tried to solve.
The matrix in the attachment has no inverse. Explain how you can determine the value of x. Then find x.
I tried cross multiplying.
3*2/3=4x
6/3=4x
2=4x
x=2/4
x=1/2