Matrix Representations of the Poincare Group

[cuallito]

I'm trying to 'see' what the generators of the Poincare Group are. From what I understand, it has 10 generators. 6 are the Lorentz generators for rotations/boosts, and 4 correspond to translations in ℝ^1,3 since PoincareGroup = ℝ^1,3 ⋊ SO(1,3).

The 6 Lorentz generators are easy enough to find in the literature. They are:

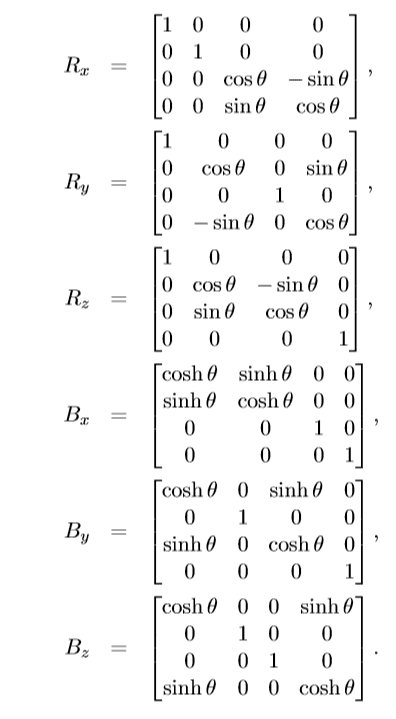
I cannot find the ℝ^1,3 generators explicitly stated anywhere. My naive guess is that since the other four generators correspond to translations in ℝ^1,3, we get the other 4 generators by exponentiating the 4 translation matrices for ℝ^1,3.

Is that correct?

 

[A. Neumaier]

To get the Poincare group you need to take a semidirect product with the translation group. This means that you get a 5-dimensional representation by 5x5 matrices $\pmatrix{A & t \cr 0 & 1}$, where $A$ is a Lorentz transformation and $t$ a translation vector. The relevant orbit of this matrix action is the set of 5D vectors
$\pmatrix{x \cr 1}$, where $x$ is a point in Minkowski space.

 

[cuallito]

Thanks Prof. Neumaier, so would the generators then be the six rotations/boosts

$$
R_x = \begin{pmatrix}
1 & 0 & 0 & 0 & 0\\
0 & 1 & 0 & 0 & 0\\
0 & 0 & cos \theta & -sin \theta & 0\\
0 & 0 & sin \theta & cos \theta & 0\\
0 & 0 & 0 & 0 & 1
\end{pmatrix}

~
R_y = \begin{pmatrix}
1 & 0 & 0 & 0 & 0\\
0 & cos\theta & 0 & sin\theta & 0\\
0 & 0 & 1 & 0 & 0\\
0 & -sin\theta & 0 & cos\theta & 0\\
0 & 0 & 0 & 0 & 1
\end{pmatrix}

~
R_z =
\begin{pmatrix}
1 & 0 & 0 & 0 & 0\\
0 & cos\theta & -sin\theta & 0 & 0\\
0 & sin\theta & cos\theta & 0 & 0\\
0 & 0 & 0 & 1 & 0\\
0 & 0 & 0 & 0 & 1
\end{pmatrix}

$$
$$

B_x =
\begin{pmatrix}
cosh \theta & sinh \theta & 0 & 0 & 0\\
sinh \theta & cosh \theta & 0 & 0 & 0\\
0 & 0 & 1 & 0 & 0\\
0 & 0 & 0 & 1 & 0\\
0 & 0 & 0 & 0 & 1
\end{pmatrix}

~
B_y = \begin{pmatrix}
cosh \theta & 0 & sinh \theta & 0 & 0\\
0 & 1 & 0 & 0 & 0\\
sinh \theta & 0 & cosh \theta & 0 & 0\\
0 & 0 & 0 & 1 & 0\\
0 & 0 & 0 & 0 & 1
\end{pmatrix}

~
B_z = \begin{pmatrix}
cosh \theta & 0 & 0 & sinh \theta & 0\\
0 & 1 & 0 & 0 & 0\\
0 & 0 & 1 & 0 & 0\\
sinh \theta & 0 & 0 & cosh \theta & 0\\
0 & 0 & 0 & 0 & 1
\end{pmatrix}

$$

Plus the four the translations represented like this?

$$ T_t = \begin{pmatrix}1 & 0 & 0 & 0 & -c t\\ 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\end{pmatrix}

T_x = \begin{pmatrix}
1 & 0 & 0 & 0 & 0\\
0 & 1 & 0 & 0 & x\\
0 & 0 & 1 & 0 & 0\\
0 & 0 & 0 & 1 & 0\\
0 & 0 & 0 & 0 & 1
\end{pmatrix}
~
T_y = \begin{pmatrix}
1 & 0 & 0 & 0 & 0\\
0 & 1 & 0 & 0 & 0\\
0 & 0 & 1 & 0 & y\\
0 & 0 & 0 & 1 & 0\\
0 & 0 & 0 & 0 & 1
\end{pmatrix}
~
T_z = \begin{pmatrix}
1 & 0 & 0 & 0 & 0\\
0 & 1 & 0 & 0 & 0\\
0 & 0 & 1 & 0 & 0\\
0 & 0 & 0 & 1 & z\\
0 & 0 & 0 & 0 & 1
\end{pmatrix}

$$

 

[A. Neumaier]

would the generators then be the six rotations/boosts
Plus the four the translations represented like this?

Generators have no free parameters left but each of your matrices contains such a parameter.

What you wrote down is not describing generators but the 1-parameter groups they are generating. Taking the derivatives at zero gives the generators.

 

[cuallito]

Thanks professor, like a true scientist, I'm always happy to know when I'm wrong