- #1
ChristinaMaria
- 10
- 0
Hello!
I have been working on this problem for a while. Apparently I've found the right answer, but I don't understand why it is correct.
Find the maximum and minimum value for the function
ƒ(x, y) = 2xy - 13x
on the rectangle
-3 ≤ x ≤ 3
0 ≤ y ≤ 2
Critical points:
ƒ(x, 0) = -13x
ƒ(-3, 0) = 39
ƒ(3, 0) = -39
⇒ ƒ has maximum and minimum values on the rectangle at ƒ(-3, 0) = 39 and ƒ(3, 0) = -39.
--------
I checked my answer and it is correct, but I don't completely understand why. I plotted the function ƒ(x,y) =2xy - 13x and the maxima and minima A=(-3,0) and B=(3,0). The points are not even on the curve. How can the function then have maximum and minimum values at these points?
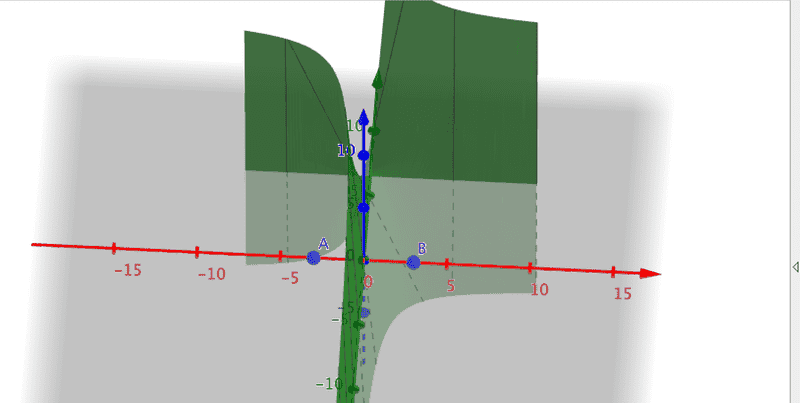
I have been working on this problem for a while. Apparently I've found the right answer, but I don't understand why it is correct.
Homework Statement
Find the maximum and minimum value for the function
ƒ(x, y) = 2xy - 13x
on the rectangle
-3 ≤ x ≤ 3
0 ≤ y ≤ 2
The Attempt at a Solution
Critical points:
- A) ∂f/∂x = 0 = 2x - 13
- B) ∂f/∂y = 0 = 2y
- A) ∂f/∂x = 0 ⇒ x = 13/2 ⊄ [-3, 3] None within the boundary
- B) ∂f/∂y = 0 ⇒ y = 0 ∈ [0, 2], Ok!
ƒ(x, 0) = -13x
ƒ(-3, 0) = 39
ƒ(3, 0) = -39
⇒ ƒ has maximum and minimum values on the rectangle at ƒ(-3, 0) = 39 and ƒ(3, 0) = -39.
--------
I checked my answer and it is correct, but I don't completely understand why. I plotted the function ƒ(x,y) =2xy - 13x and the maxima and minima A=(-3,0) and B=(3,0). The points are not even on the curve. How can the function then have maximum and minimum values at these points?