Max Impulse on a pendulum

[PakBosMuda]

TL;DR Summary: An impulse is given to the pendulum so that it moves in 3 dimensions. What equations apply throughout its motion?

A particle of mass $m$ is suspended from a string of length $\ell$. The string is then deflected at an angle $\theta$, where the particle and string are in the XY-plane.

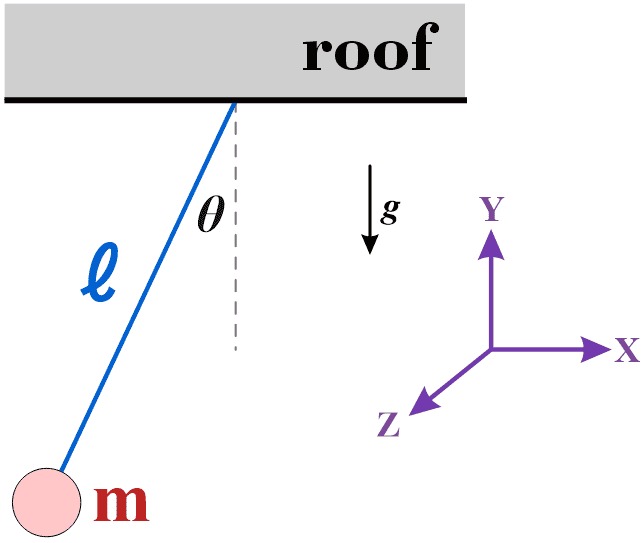
What is the maximum impulse in the Z-axis direction so that the particle does not hit the roof?
________________________________________________________________________
---------------------------------------------------------------------------

What I already know (CMIIW):

1. Throughout its motion, the energy of the particle is conserved:
$$E_{i} = E_{r}$$
$$PE_{i} + KE_{i} = PE_{r} + KE_{r}$$
$$-m.g. \ell . \cos \theta + \frac{1}{2} . m . v_{i}^2 = 0 + \frac{1}{2} . m . v_{r}^2$$
$$v_{i}^2 = 2g. \ell . \cos \theta + v_{r}^2$$

2. The condition for a particle not to hit the roof is that its final velocity vector (when on the roof) is in the XZ-plane $\rightarrow \left( v_r \right) _y = 0$

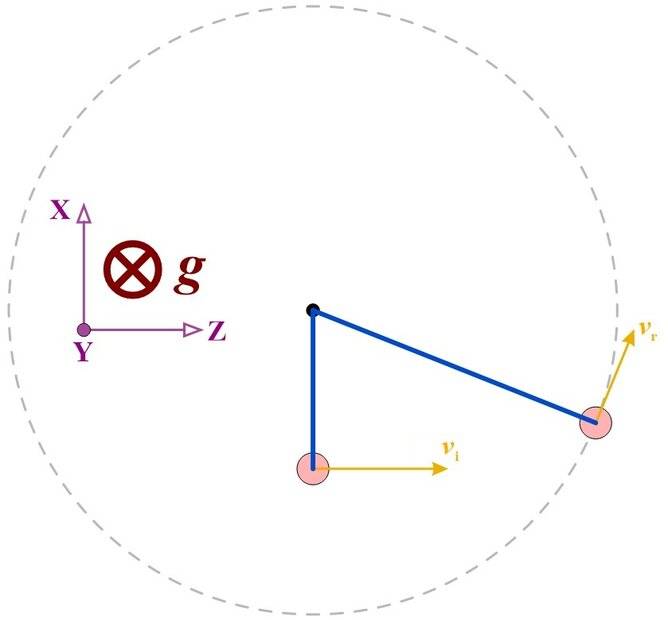
3. Angular momentum is NOT CONSERVED, because the weight creates torque (as well as linear momentum).

There are 2 unknown variables : $v_i$ and $v_r$, while the only equation I have is energy conservation. What am I missing?

 

[Orodruin]

This is nothing but a spherical pendulum. Angular momentum in what you have lanelef the y-direction is conserved due to rotational symmetry about the y-axis.

Also, please do not use periods as multiplication in $\LaTeX$. Leaving the multiplication operator is fine.