james weaver
- 28
- 4
Homework Statement:: project not homework
Relevant Equations:: vectors
Hi,I am trying to determine the maximum linear velocity of a propeller tip when subject to flowing water with velocity ##\vec V##. For simplicity, I will assume that rotational inertial is negligible. The drawing below shows the tip of a propeller blade as viewed directly level from the side. If the following diagram is correct, it implies that the maximum of ##\vec Vsin\theta cos\theta## will occur when ##\theta## is at 45 degrees, and will be equal to exactly ##\frac 1 2\ \vec V##
The relationship seems reasonable as ##\vec Vsin\theta cos\theta## is zero when ##\theta## equals 0 or 90, which is expected.
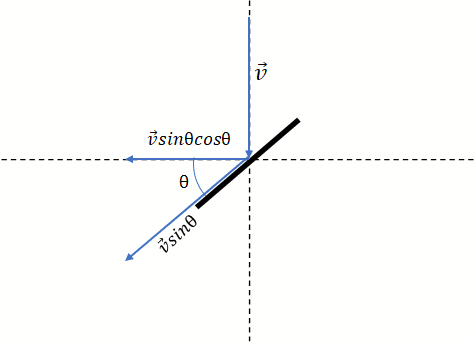
Relevant Equations:: vectors
Hi,I am trying to determine the maximum linear velocity of a propeller tip when subject to flowing water with velocity ##\vec V##. For simplicity, I will assume that rotational inertial is negligible. The drawing below shows the tip of a propeller blade as viewed directly level from the side. If the following diagram is correct, it implies that the maximum of ##\vec Vsin\theta cos\theta## will occur when ##\theta## is at 45 degrees, and will be equal to exactly ##\frac 1 2\ \vec V##
The relationship seems reasonable as ##\vec Vsin\theta cos\theta## is zero when ##\theta## equals 0 or 90, which is expected.