maxim07
- 53
- 8
Summary:: Question: a car of mass 800kg, 3600N driving force experiences resistive forces of 120v Accelerates from rest. Form equation and show max speed is 30 ms^-1, assuming driving force does not change.
my attempt at a solution -I can not see how to rectify it as I don’t think I did anything wrong in the first steps. Thanks.
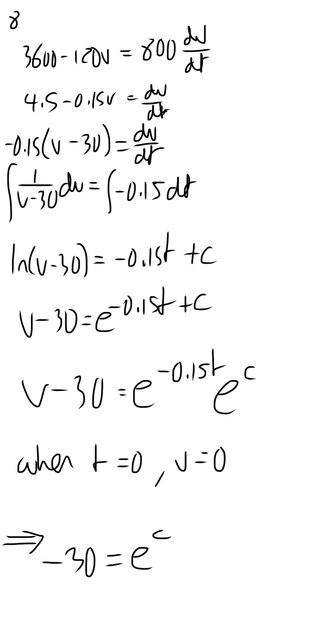
my attempt at a solution -I can not see how to rectify it as I don’t think I did anything wrong in the first steps. Thanks.