Maximisation Question: Find Largest Capacity

[Nemo1]

Hi Community,

I have this question and I would like to share my working out so far and some help on how to proceed would be appreciated.
View attachment 5548View attachment 5549

So far I have determined for Part a:

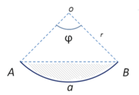
Circumference of a circle is = $$2 \pi r$$ and to write a formula relating $\varphi$ $a$ and $r$ with $a$ being the length of the line as shown on the graph not the area.

I get $a=\varphi \cdot radians$ then I solve for $$\varphi=\frac{a}{radians}$$

For Part b:

If I treat $a$ as a straight line and look to solve this problem as a right angle triangle using the equation in Part a I get:

$$Sin\left(\frac{\varphi}{2}\right)=\frac{\frac{a}{2}}{radians}$$ solving for $\varphi$ should give me the maximum value $\varphi$ can take.

$$\varphi = 2arcsin\left(\frac{a}{2r}\right)$$

For Part c:

The area of a circle is $\pi r^2$ writing the area of a slice of a circle in terms of $\varphi$ I get $$S=\frac{\varphi}{2}\cdot r^2$$

In order to write $S$ in terms of $\varphi$ and $a$ only (eliminate $r$) $$S=\frac{\varphi}{2}\left(\frac{a}{\varphi}\right)^{\!{2}}$$ which simplifies to $$S=\frac{a^2}{2 \varphi}$$

For Part d:
The area of a triangle is $$\frac{1}{2}\cdot base \cdot height$$

Using trigonometry I can use $Cos$ to get the following $$Cos\left(\frac{\varphi}{2}\right)=\frac{height}{r}\cdot Sin\left(\frac{\varphi}{2}\right)=\frac{base}{2r}$$

Solving to get the area of the triangle $OAB$ I get $$area(T)= 2r^2 Cos\left(\frac{\varphi}{2}\right)\cdot Sin\left(\frac{\varphi}{2}\right)$$

For Part e:
By subtracting the area of the triangle from the circle slice is equal to $$H=\frac{a^2}{2 \varphi} - 2r^2 \cdot Cos\left(\frac{\varphi}{2}\right)\cdot Sin\left(\frac{\varphi}{2}\right)$$

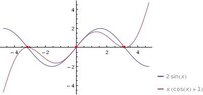
It is from this point I am stuck, I am unsure if my working so far makes sense and also how to arrive at $$2 Sin \varphi = \varphi(1+ Cos \varphi)$$

When I graph the given equation $$2 Sin \varphi = \varphi(1+ Cos \varphi)$$ I get:
View attachment 5547
(I have used $x$ in place of $\varphi$ to get the graph to work.)

I can see that $0$ and $\pi$ are solutions.

I will need to graph this into excel and argue that because the two functions intercept at $0$ and $\pi$ they are both valid solutions to this equation.

For Part h: I am unsure of how to find the largest capacity where the sheet is bent into a half-circle. My intuition says it is where $\varphi$ is equal to $\pi$ $radians$ as $2\pi$ $radians$ is equal to a full revolution of a circle.

I hope I have explained my reasoning well enough to make sense and I look forward to hearing some thoughts.

Cheers Nemo

 

[MarkFL]

For part a), we can use the arc-length formula for a circular arc to state:

$$a=r\varphi$$

For part b), I would say $\varphi_{\max}=\pi$, in which case we have a half-pipe. It could be bent more, but then it wouldn't truly be an open-top trough.

For part c), we may use the formula for the area of a circular sector and state:

$$S=\frac{1}{2}r^2\varphi$$

And so, using $$a=r\varphi\implies r=\frac{a}{\varphi}$$ (from part a)), there results:

$$S=\frac{1}{2}\left(\frac{a}{\varphi}\right)^2\varphi=\frac{a^2}{2\varphi}$$

For part d), using the formula for the area of a triangle, we may write:

$$T=\frac{1}{2}r^2\sin\left(\varphi\right)=\frac{1}{2}\left(\frac{a}{\varphi}\right)^2\sin\left(\varphi\right)=\frac{a^2\sin\left(\varphi\right)}{2\varphi^2}$$

And then for part e), we have:

$$H=S-T=\frac{a^2}{2\varphi}-\frac{a^2\sin\left(\varphi\right)}{2\varphi^2}=\frac{a^2}{2\varphi^2}\left(\varphi-\sin\left(\varphi\right)\right)$$

Now, can you compute $$\d{H}{\varphi}$$?

 

[Nemo1]

For part a), we can use the arc-length formula for a circular arc to state:

$$a=r\varphi$$

For part b), I would say $\varphi_{\max}=\pi$, in which case we have a half-pipe. It could be bent more, but then it wouldn't truly be an open-top trough.

For part c), we may use the formula for the area of a circular sector and state:

$$S=\frac{1}{2}r^2\varphi$$

And so, using $$a=r\varphi\implies r=\frac{a}{\varphi}$$ (from part a)), there results:

$$S=\frac{1}{2}\left(\frac{a}{\varphi}\right)^2\varphi=\frac{a^2}{2\varphi}$$

For part d), using the formula for the area of a triangle, we may write:

$$T=\frac{1}{2}r^2\sin\left(\varphi\right)=\frac{1}{2}\left(\frac{a}{\varphi}\right)^2\sin\left(\varphi\right)=\frac{a^2\sin\left(\varphi\right)}{2\varphi^2}$$

And then for part e), we have:

$$H=S-T=\frac{a^2}{2\varphi}-\frac{a^2\sin\left(\varphi\right)}{2\varphi^2}=\frac{a^2}{2\varphi^2}\left(\varphi-\sin\left(\varphi\right)\right)$$

Now, can you compute $$\d{H}{\varphi}$$?

Hi Mark,

I have been working thru the first stages of the problems and concur with your answers. Once I know what formulas to use on the problems it makes a lot more sense. Unfortunately for me, I have not been shown these formulas like the arc-length formula and so forth hence my confusion.

On differentiating $$\frac{a^2}{2\varphi^2}\left(\varphi-\sin\left(\varphi\right)\right)$$

I have looked back thru all of my notes from my lectures and also the course I did last year and I cannot see how to compute $$\d{H}{\varphi}$$

All of the problems I have had so far in regards to differentiation have always been w.r.t $x$ and use the rules like chain, quotient and so forth.

My current thoughts on solving this is that we are solving $H$ w.r.t $\varphi$ with $H$ being the whole function $$\frac{a^2}{2\varphi^2}\left(\varphi-\sin\left(\varphi\right)\right)$$

So I get $$\frac{2a}{4\varphi}\left(\varphi-\cos\left(\varphi\right)\right)$$

Is it the same method as $$\d{}{x}$$ but solving for $$\d{}{\varphi}$$?

Also on the notation aspect, when we write $$\d{H}{\varphi}$$ does it mean that we are solving the function $H$ w.r.t $\varphi$?

Could you please show me what the theorem for solving the last bit and I will have a go at applying it to the problem.

Much appreciation.

Cheers Nemo.

 

[MarkFL]

Hello, Nemo! :D

We have:

$$H=\frac{a^2}{2\varphi^2}\left(\varphi-\sin\left(\varphi\right)\right)$$

Now, we must realize here that $a$ is a parameter, which is an unspecified constant. It doesn't vary in the way $r$ and $\varphi$ do with respect to the curvature of the sheet. So, when computing $$\d{H}{\varphi}$$, we treat $a$ just as we would a numeric constant.

So, what we need to use here to compute the required derivative (to differentiate $H$ w.r.t $\varphi$), is to use the product rule. First, let's write $H$ as:

$$H=\frac{a^2}{2}\varphi^{-2}\left(\varphi-\sin\left(\varphi\right)\right)$$

Hence:

$$\d{H}{\varphi}=\frac{a^2}{2}\left(\varphi^{-2}\left(1-\cos\left(\varphi\right)\right)-2\varphi^{-3}\left(\varphi-\sin\left(\varphi\right)\right)\right)=\frac{a^2}{2\varphi^3}\left(2\sin\left(\varphi\right)-\varphi\left(1+\cos\left(\varphi\right)\right)\right)$$

Something troubling me here, is that you are told to equate this derivative to zero, and confirm that this implies:

$$2\sin\left(\varphi\right)=\varphi\left(1+\cos\left(\varphi\right)\right)$$

and that:

$$\varphi\in\{0,\pi\}$$

are solutions, but when $\varphi=0$, we have:

$$\d{H}{\varphi}=\frac{0}{0}$$

which is an indeterminate form. Now, if we repeatedly apply L'Hôpital's Rule to the limit:

$$\lim_{\varphi\to0}\d{H}{\varphi}$$

We do in fact find this limit converges to zero. I just wanted to point out that a key detail has been glossed over here. :)

 

[Nemo1]

Hello, Nemo! :D

We have:

$$H=\frac{a^2}{2\varphi^2}\left(\varphi-\sin\left(\varphi\right)\right)$$

Now, we must realize here that $a$ is a parameter, which is an unspecified constant. It doesn't vary in the way $r$ and $\varphi$ do with respect to the curvature of the sheet. So, when computing $$\d{H}{\varphi}$$, we treat $a$ just as we would a numeric constant.

So, what we need to use here to compute the required derivative (to differentiate $H$ w.r.t $\varphi$), is to use the product rule. First, let's write $H$ as:

$$H=\frac{a^2}{2}\varphi^{-2}\left(\varphi-\sin\left(\varphi\right)\right)$$

Hence:

$$\d{H}{\varphi}=\frac{a^2}{2}\left(\varphi^{-2}\left(1-\cos\left(\varphi\right)\right)-2\varphi^{-3}\left(\varphi-\sin\left(\varphi\right)\right)\right)=\frac{a^2}{2\varphi^3}\left(2\sin\left(\varphi\right)-\varphi\left(1+\cos\left(\varphi\right)\right)\right)$$

Something troubling me here, is that you are told to equate this derivative to zero, and confirm that this implies:

$$2\sin\left(\varphi\right)=\varphi\left(1+\cos\left(\varphi\right)\right)$$

and that:

$$\varphi\in\{0,\pi\}$$

are solutions, but when $\varphi=0$, we have:

$$\d{H}{\varphi}=\frac{0}{0}$$

which is an indeterminate form. Now, if we repeatedly apply L'Hôpital's Rule to the limit:

$$\lim_{\varphi\to0}\d{H}{\varphi}$$

We do in fact find this limit converges to zero. I just wanted to point out that a key detail has been glossed over here. :)

Hi Mark,

So I can see by using one of the exponent rules you have moved the $$\frac{a^2}{2\varphi^2}$$ out from the denominator to get $$\frac{a^2}{2}\varphi^{-2}$$ to rearrange the equation.

Using the product rule $$f^{\prime}(x)= f(x)\cdot g^{\prime}(x)+f^{\prime}(x)\cdot g(x)$$

Where:
$$f(x)= \varphi^{-2}$$
$$f^{\prime}(x)= -2\varphi^{-3}$$
$$g(x)= \left(\varphi-\sin\left(\varphi\right)\right)$$
$$g^{\prime}(x)= \left(1-\cos\left(\varphi\right)\right)$$

To get $$\d{H}{\varphi}=\frac{a^2}{2}\left(\varphi^{-2}\left(1-\cos\left(\varphi\right)\right)-2\varphi^{-3}\left(\varphi-\sin\left(\varphi\right)\right)\right)$$

Which solves to

$$\frac{a^2}{2\varphi^3}\left(2\sin\left(\varphi\right)-\varphi\left(1+\cos\left(\varphi\right)\right)\right)$$

Now in your response you stated that $a$ is a parameter, which is an unspecified constant. Does this mean we can set it to equal Zero like you would when taking the derivative of a constant? Or is it the constant we are setting to Zero in $$\d{H}{\varphi}=0$$

My last bit of confusion is around the use of L'Hôpital's Rule as I have never used it and also how does $$\frac{a^2}{2\varphi^3}\left(2\sin\left(\varphi\right)-\varphi\left(1+\cos\left(\varphi\right)\right)\right)$$ end up becoming $$2 sin(\varphi)=\varphi(1+cos \varphi)$$

I am sorry if I am asking Algebra 101 questions but it's my greatest weak point especially with trig functions.

Cheers Nemo.

 

[MarkFL]

...Now in your response you stated that $a$ is a parameter, which is an unspecified constant. Does this mean we can set it to equal Zero like you would when taking the derivative of a constant? Or is it the constant we are setting to Zero in $$\d{H}{\varphi}=0$$

No, all we need to know about $a$ is that it represents the width of the sheet, and so it can be any value greater than zero. But we may equate it to any positive value. We are only interested in how $\varphi$ varies with respect to the curvature of the sheet, and the resulting volume of the trough.

My last bit of confusion is around the use of L'Hôpital's Rule as I have never used it and also how does $$\frac{a^2}{2\varphi^3}\left(2\sin\left(\varphi\right)-\varphi\left(1+\cos\left(\varphi\right)\right)\right)$$ end up becoming $$2 sin(\varphi)=\varphi(1+cos \varphi)$$

If I recall correctly, L'Hôpital's Rule is taught in the second semester of calculus, I simply wanted you to be aware that there was a bit more going on there.

Now, if we have:

$$\d{H}{\varphi}=\frac{a^2}{2\varphi^3}\left(2\sin\left(\varphi\right)-\varphi\left(1+\cos\left(\varphi\right)\right)\right)=0$$

And we ignore the denominator, and set the variable factor in the numerator to zero, we get:

$$2\sin\left(\varphi\right)-\varphi\left(1+\cos\left(\varphi\right)\right)=0$$

And by adding $$\varphi\left(1+\cos\left(\varphi\right)\right)$$ to both sides, we then have:

$$2\sin\left(\varphi\right)=\varphi\left(1+\cos\left(\varphi\right)\right)$$

 

[Nemo1]

Thanks Mark,

Took a bit of work in looking at the algebra but I think I have a decent grasp. I will need to stay sharp on these kinds of questions of the next few years to really understand and solve them with confidence.

Cheers Nemo