Maximize Trapezoid Area with 3 Equal Sides | Leprofece Answer

[MarkFL]

Here is the question:

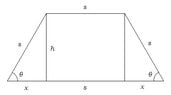
Between all the trapezoids that have three equal sides, to determine which has the maximum area.?

Answer: the regular semi-hexagon.

You must demonstrate or show it.

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello leprofece,

Let's first draw a diagram:

View attachment 1655

The area $A$ of the trapezoid is the area of the middle rectangle and the areas of the right triangles on either side:

\(\displaystyle A=hs+2\left(\frac{1}{2}hs\cos(\theta) \right)=hs\left(1+\cos(\theta) \right)\)

Now we have \(\displaystyle h=s\sin(\theta)\) hence:

\(\displaystyle A(\theta)=s^2\sin(\theta)\left(1+\cos(\theta) \right)\)

Differentiating with respect to $\theta$ and equating the result to zero, we find:

\(\displaystyle A'(\theta)=s^2\left(-\sin^2(\theta)+\cos(\theta)\left(1+\cos(\theta) \right) \right)=s^2\left(2\cos^2(\theta)+\cos(\theta)-1 \right)=s^2\left(2\cos(\theta)-1 \right)\left(\cos(\theta)+1 \right)=0\)

Since $0<s$, and $0\le\theta<\pi$ this implies:

\(\displaystyle \cos(\theta)=\frac{1}{2}\,\therefore\,\theta=\frac{\pi}{3}\)

Using the first derivative test, we find:

\(\displaystyle A'(0)=2s^2>0\)

\(\displaystyle A'\left(\frac{\pi}{2} \right)=-s^2<0\)

Thus we conclude the critical value \(\displaystyle \theta=\frac{\pi}{3}\) is at a maximum for the area, and we can easily see this gives us a trapezoid that is a semi-hexagon.