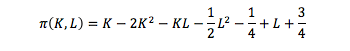Maximizing Profit Function Of Two Variables

[MioMio]

Yes, please help me solve! Explain it very explicitly with equations and not just text.

1) Find the combination of K and L that ensures the maximum profit and find the maximum profit. The profit is given by the following function:where:

 

[MarkFL]

First you need to find the critical points, which will be the solutions of:

\[\pi_K(K,L)=0\]
\[\pi_L(K,L)=0\]

Then you need to use the second partials test for relative extrema. What do you have so far?

 

[MioMio]

I have nothing. To be honest with you, I am totally lost. Could you explain it so that even a stupid person might understand it?

I'm sorry to bother you.

 

[MarkFL]

I have nothing. To be honest with you, I am totally lost. Could you explain it so that even a stupid person might understand it?

I'm sorry to bother you.

Okay, we are given the profit function:

$$\pi(K,L)=K-2K^2-KL-\frac{1}{2}L^2-\color{red}\frac{1}{4}\color{black}+L+\color{red}\frac{3}{4}$$

After having looked more closely at the profit function, is seems odd to me that there are two constant terms that have not been combined (in red). Before we proceed, are you certain the profit function is stated correctly?

 

[MioMio]

I'm 100% sure

 

[MarkFL]

I'm 100% sure

Okay, then let's clean it up by combining those term, so that we have:

$$\pi(K,L)=K-2K^2-KL-\frac{1}{2}L^2+L+\frac{1}{2}$$

So, first let's compute the first partial with respect to $K$, denoted by:

$$\pi_K(K,L)$$ or $$\pd{\pi}{K}$$

We use the familiar rules of differentiation, while treating $L$ as a constant. What do you get for this partial?

 

[MioMio]

I have actually just found an example in my textbook that resembles this one, so I think I understand it now. I'm really sorry for taking your time, but I hope it's all right if I return to you if I have any questions. And thank you again for taking the time to help me, it means a lot.

 

[MarkFL]

I have actually just found an example in my textbook that resembles this one, so I think I understand it now. I'm really sorry for taking your time, but I hope it's all right if I return to you if I have any questions. And thank you again for taking the time to help me, it means a lot.

Glad to help, and certainly if you have any questions when you are working this problem, please don't hesitate to ask. :D