Maximizing Pulling Force with Static Friction

[Curieuse]

Homework Statement

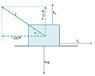
An initially stationary box of sand is to be pulled across a floor by means of a cable in which the tension should not exceed 1100 N. The coefficient of static friction between the box and the floor is 0.35.
(a) What should be the angle between the cable and the horizontal in order to pull the greatest amount of sand, and
(b) What is the weight of the sand and box in that situation?

Homework Equations

F=ma
f_s-max = F_Nμ_s

The Attempt at a Solution

Because the block has to move after all,
the applied force's x-component must be greater than the frictional force that will oppose it by acting in the opposite direction with a maximum magnitude as static frictional force max f_s-max.
So, T cosθ > μ_s(mg-T sinθ)
rewrite, T(cosθ + μ_ssinθ)> 3.43 m
Besides 0 < T < 1100 N
So, 0 < T(cosθ + μ_ssinθ) < 1100(T(cosθ + μ_ssinθ))
And if 3.43 m is already lesser than T(cosθ + μ_ssinθ),
It surely is lesser than 1100(T(cosθ + μ_ssinθ))..
rewriting i get,
cosθ + 0.35 sinθ > 3.1*10^-3 m------------------------(1)
Here, I got a gut feeling and a bit of crooked logic telling me that since the RHS is lesser than the LHS, I should probably be finding the maximum value of the LHS, which would give me the corresponding maximum value for the RHS.
So, I did the maxima for the LHS and got θ=19.3°
this, i resubstituted in (1) to get
m < 341.9 kg.
And so the (a) 19.3°
and (b) weight of the load so (341.9)(9.8)=3.35*10³
which tallied with the answers at the back.
BUT is there another method to attack the problem? Is my logic crooked? Any better explanation for the key step where i find θ using maxima? Any advice to tidy up my reasoning in the rest of the solution is also highly welcome! Thanks!

 

[PhanthomJay]

looks real good! I guess you could take the second derivative to be sure you have a max and not a min, which maybe you did, as you did not show calcs for determining the angle for max mass.

 

[Curieuse]

Yes, @PhantomJay! Thanks!