Maximizing the volume of a beam cut from a cylindrical trunk

[leprofece]

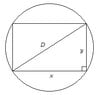
what are the dimensions of rectangular beam of volume maximum that can be cut from a trunk in diameter "D" and length "L", assuming that the trunk has the shaped of a straight circular cylinder shape?

Answer Width =lenght

 

[MarkFL]

Re: max and min 295

What have you tried?

Do you recognize that this problem boils down to maximizing the area of a rectangle inscribed within a circle?

As always, what is your constraint? What is your objective function?

Hint: look at the diagonal of the rectangle and how it relates to the diameter of the circle. And then how do the sides of the rectangle relate to its diagonal?

 

[leprofece]

Re: max and min 295

What have you tried?

Do you recognize that this problem boils down to maximizing the area of a rectangle inscribed within a circle?

As always, what is your constraint? What is your objective function?

Hint: look at the diagonal of the rectangle and how it relates to the diameter of the circle. And then how do the sides of the rectangle relate to its diagonal?

It shall be a square beam of side equal to D/2.
Length equal to length of trunk.

If it is the area of a rectangle inscribed within a circle?

a = pir
and R²= x²-r²
r= sqrt(R²-x²)
A=2pisqrt(R²-x²)
I derive A and I must get the answer

 

[MarkFL]

Re: max and min 295

Here is a cross-section:

View attachment 2086

Our objective function is the area of the rectangle:

$$A(x,y)=xy$$

Subject to the constraint (by Pythagoras):

$$x^2+y^2=D^2$$

So, solve the constraint for either variable, and substitute for that variable into the objective function so that you only have one variable, and then maximize.

 

[leprofece]

Re: max and min 295

Here is a cross-section:

View attachment 2086

Our objective function is the area of the rectangle:

$$A(x,y)=xy$$

Subject to the constraint (by Pythagoras):

$$x^2+y^2=D^2$$

So, solve the constraint for either variable, and substitute for that variable into the objective function so that you only have one variable, and then maximize.

Ok I got y = x = D/sqrt(2)